Circumference and Diameter: A History of Pi from Antiquity to the Modern World Brewminate: A Bold Blend of News and Ideas

**Archimedes developed the polygonal approach to approximating π. / Courtesy Gemäldegalerie Alte Meister, Wikimedia Commons**

The calculation of π was revolutionized by the development of infinite series techniques in the 16th and 17th centuries.

Curated/Reviewed by Matthew A. McIntosh
Public Historian
Brewminate

Antiquity

The best-known approximations to π dating before the Common Era were accurate to two decimal places; this was improved upon in Chinese mathematics in particular by the mid-first millennium, to an accuracy of seven decimal places. After this, no further progress was made until the late medieval period.

The earliest written approximations of π are found in Babylon and Egypt, both within one percent of the true value. In Babylon, a clay tablet dated 1900–1600 BC has a geometrical statement that, by implication, treats π as 25/8 = 3.125.^[41] In Egypt, the Rhind Papyrus, dated around 1650 BC but copied from a document dated to 1850 BC, has a formula for the area of a circle that treats π as (169)2≈3.16 ${\textstyle {\bigl (}{\frac {16}{9}}{\bigr )}^{2}\approx 3.16}$ .^[32][41] Although some pyramidologists have theorized that the Great Pyramid of Giza was built with proportions related to π, this theory is not widely accepted by scholars.^[42] In the Shulba Sutras of Indian mathematics, dating to an oral tradition from the first or second millennium BC, approximations are given which have been variously interpreted as approximately 3.08831, 3.08833, 3.004, 3, or 3.125.^[43]

Polygon Approximation Era

Overview

**π can be estimated by computing the perimeters of circumscribed and inscribed polygons. / Courtesy Wikimedia Commons**

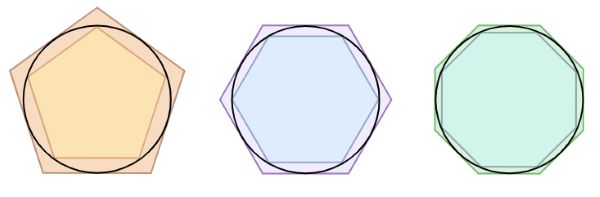
The first recorded algorithm for rigorously calculating the value of π was a geometrical approach using polygons, devised around 250 BC by the Greek mathematician Archimedes, implementing the method of exhaustion.^[44] This polygonal algorithm dominated for over 1,000 years, and as a result π is sometimes referred to as Archimedes’s constant.^[45] Archimedes computed upper and lower bounds of π by drawing a regular hexagon inside and outside a circle, and successively doubling the number of sides until he reached a 96-sided regular polygon. By calculating the perimeters of these polygons, he proved that 223/71 < π < 22/7 (that is, 3.1408 < π < 3.1429).^[46] Archimedes’ upper bound of 22/7 may have led to a widespread popular belief that π is equal to 22/7.^[47] Around 150 AD, Greek-Roman scientist Ptolemy, in his Almagest, gave a value for π of 3.1416, which he may have obtained from Archimedes or from Apollonius of Perga.^[48][49] Mathematicians using polygonal algorithms reached 39 digits of π in 1630, a record only broken in 1699 when infinite series were used to reach 71 digits.^[50]

In ancient China, values for π included 3.1547 (around 1 AD), 10 ${\sqrt {10}}$ (100 AD, approximately 3.1623), and 142/45 (3rd century, approximately 3.1556).^[51] Around 265 AD, the Wei Kingdom mathematician Liu Hui created a polygon-based iterative algorithm and used it with a 3,072-sided polygon to obtain a value of π of 3.1416.^[52][53] Liu later invented a faster method of calculating π and obtained a value of 3.14 with a 96-sided polygon, by taking advantage of the fact that the differences in area of successive polygons form a geometric series with a factor of 4.^[52] The Chinese mathematician Zu Chongzhi, around 480 AD, calculated that 3.1415926<Pi<3.1415927 $3.1415926<\pi <3.1415927$ and suggested the approximations Pi≈355113=3.14159292035… ${\textstyle \pi \approx {\frac {355}{113}}=3.14159292035...}$ and Pi≈227=3.142857142857… ${\textstyle \pi \approx {\frac {22}{7}}=3.142857142857...}$ , which he termed the Milü (”close ratio”) and Yuelü (“approximate ratio”), respectively, using Liu Hui’s algorithm applied to a 12,288-sided polygon. With a correct value for its seven first decimal digits, this value remained the most accurate approximation of π available for the next 800 years.^[54]

The Indian astronomer Aryabhata used a value of 3.1416 in his Āryabhaṭīya (499 AD).^[55] Fibonacci in c. 1220 computed 3.1418 using a polygonal method, independent of Archimedes.^[56] Italian author Dante apparently employed the value 3+210≈3.14142 ${\textstyle 3+{\frac {\sqrt {2}}{10}}\approx 3.14142}$ .^[56]

The Persian astronomer Jamshīd al-Kāshī produced nine sexagesimal digits, roughly the equivalent of 16 decimal digits, in 1424, using a polygon with 3×228 ${\textstyle 3\times 2^{28}}$ sides,^[57][58] which stood as the world record for about 180 years.^[59] French mathematician François Viète in 1579 achieved nine digits with a polygon of 3×217 ${\textstyle 3\times 2^{17}}$ sides.^[59] Flemish mathematician Adriaan van Roomen arrived at 15 decimal places in 1593.^[59] In 1596, Dutch mathematician Ludolph van Ceulen reached 20 digits, a record he later increased to 35 digits (as a result, π was called the “Ludolphian number” in Germany until the early 20th century).^[60] Dutch scientist Willebrord Snellius reached 34 digits in 1621,^[61] and Austrian astronomer Christoph Grienberger arrived at 38 digits in 1630 using 10⁴⁰ sides.^[62] Christiaan Huygens was able to arrive at 10 decimal places in 1654 using a slightly different method equivalent to Richardson extrapolation.^[63][64]

Infinite Series

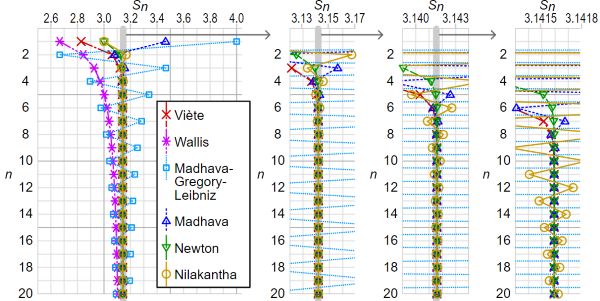
The calculation of π was revolutionized by the development of infinite series techniques in the 16th and 17th centuries. An infinite series is the sum of the terms of an infinite sequence. Infinite series allowed mathematicians to compute π with much greater precision than Archimedes and others who used geometrical techniques.^[65] Although infinite series were exploited for π most notably by European mathematicians such as James Gregory and Gottfried Wilhelm Leibniz, the approach also appeared in the Kerala school sometime in the 14th or 15th century.^[66][67] Around 1500 AD, a written description of an infinite series that could be used to compute π was laid out in Sanskrit verse in Tantrasamgraha by Nilakantha Somayaji.^[66] The series are presented without proof, but proofs are presented in a later work, Yuktibhāṣā, from around 1530 AD. Several infinite series are described, including series for sine (which Nilakantha attributes to Madhava of Sangamagrama), cosine, and arctangent which are now sometimes referred to as Madhava series. The series for arctangent is sometimes called Gregory’s series or the Gregory–Leibniz series.^[66] Madhava used infinite series to estimate π to 11 digits around 1400.^[68]

In 1593, François Viète published what is now known as Viète’s formula, an infinite product (rather than an infinite sum, which is more typically used in π calculations):^[69][70][71]

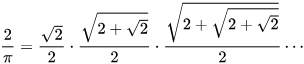
In 1655, John Wallis published what is now known as Wallis product, also an infinite product:^[69]

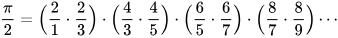
In the 1660s, the English scientist Isaac Newton and German mathematician Gottfried Wilhelm Leibniz discovered calculus, which led to the development of many infinite series for approximating π. Newton himself used an arcsine series to compute a 15-digit approximation of π in 1665 or 1666, writing, “I am ashamed to tell you to how many figures I carried these computations, having no other business at the time.”^[72]

Isaac Newton used infinite series to compute π to 15 digits, later writing “I am ashamed to tell you to how many figures I carried these computations”.^[72] / Courtesy `Institute for Mathematical Sciences, University of Cambridge`, Wikimedia Commons

In 1671, James Gregory, and independently, Leibniz in 1673, discovered the Taylor series expansion for arctangent:^[66][73][74]

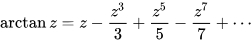
This series, sometimes called the Gregory–Leibniz series, equals Pi4 ${\textstyle {\frac {\pi }{4}}}$ when evaluated with z =1 $z=1$ .^[74] But for z =1 $z=1$ , it converges impractically slowly (that is, approaches the answer very gradually), taking about ten times as many terms to calculate each additional digit.^[75]

In 1699, English mathematician Abraham Sharp used the Gregory–Leibniz series for z =13 ${\textstyle z={\frac {1}{\sqrt {3}}}}$ to compute π to 71 digits, breaking the previous record of 39 digits, which was set with a polygonal algorithm.^[76]

In 1706, John Machin used the Gregory–Leibniz series to produce an algorithm that converged much faster:^[3][77][78]

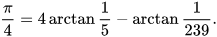
Machin reached 100 digits of π with this formula.^[79] Other mathematicians created variants, now known as Machin-like formulae, that were used to set several successive records for calculating digits of π.^[80][79]

Isaac Newton accelerated the convergence of the Gregory–Leibniz series in 1684 (in an unpublished work; others independently discovered the result):^[81]

**Leonhard Euler popularized the use of the Greek letter π in works he published in 1736 and 1748. / Courtesy Kunstmuseum Basel, Wikimedia Commons**

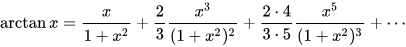
Leonhard Euler popularized this series in his 1755 differential calculus textbook, and later used it with Machin-like formulae, including Pi4=5arctan⁡17+2arctan⁡377, ${\textstyle {\tfrac {\pi }{4}}=5\arctan {\tfrac {1}{7}}+2\arctan {\tfrac {3}{77}},}$ with which he computed 20 digits of π in one hour.^[82]

Machin-like formulae remained the best-known method for calculating π well into the age of computers, and were used to set records for 250 years, culminating in a 620-digit approximation in 1946 by Daniel Ferguson – the best approximation achieved without the aid of a calculating device.^[83]

In 1844, a record was set by Zacharias Dase, who employed a Machin-like formula to calculate 200 decimals of π in his head at the behest of German mathematician Carl Friedrich Gauss.^[84]

In 1853, British mathematician William Shanks calculated π to 607 digits, but made a mistake in the 528th digit, rendering all subsequent digits incorrect. Though he calculated an additional 100 digits in 1873, bringing the total up to 707, his previous mistake rendered all the new digits incorrect as well.^[85]

Rate of Convergence

Some infinite series for π converge faster than others. Given the choice of two infinite series for π, mathematicians will generally use the one that converges more rapidly because faster convergence reduces the amount of computation needed to calculate π to any given accuracy.^[86] A simple infinite series for π is the Gregory–Leibniz series:^[87]

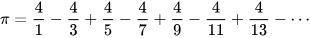
As individual terms of this infinite series are added to the sum, the total gradually gets closer to π, and – with a sufficient number of terms – can get as close to π as desired. It converges quite slowly, though – after 500,000 terms, it produces only five correct decimal digits of π.^[88]

An infinite series for π (published by Nilakantha in the 15th century) that converges more rapidly than the Gregory–Leibniz series is:^[89][90]

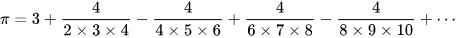
The following table compares the convergence rates of these two series:

After five terms, the sum of the Gregory–Leibniz series is within 0.2 of the correct value of π, whereas the sum of Nilakantha’s series is within 0.002 of the correct value. Nilakantha’s series converges faster and is more useful for computing digits of π. Series that converge even faster include Machin’s series and Chudnovsky’s series, the latter producing 14 correct decimal digits per term.^[86]

Irrationality and Transcendence

Not all mathematical advances relating to π were aimed at increasing the accuracy of approximations. When Euler solved the Basel problem in 1735, finding the exact value of the sum of the reciprocal squares, he established a connection between π and the prime numbers that later contributed to the development and study of the Riemann zeta function:^[91]

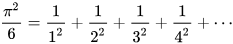
Swiss scientist Johann Heinrich Lambert in 1768 proved that π is irrational, meaning it is not equal to the quotient of any two integers.^[20]Lambert’s proof exploited a continued-fraction representation of the tangent function.^[92] French mathematician Adrien-Marie Legendre proved in 1794 that π² is also irrational. In 1882, German mathematician Ferdinand von Lindemann proved that π is transcendental,^[93] confirming a conjecture made by both Legendre and Euler.^[94][95] Hardy and Wright states that “the proofs were afterwards modified and simplified by Hilbert, Hurwitz, and other writers”.^[96]

Adoption of the Symbol π

The earliest known use of the Greek letter π to represent the ratio of a circle’s circumference to its diameter was by Welsh mathematician William Jones in 1706. / Courtesy National Portrait Gallery (London), Wikimedia Commons

In the earliest usages, the Greek letter π was used to denote the semiperimeter (semiperipheria in Latin) of a circle^[8] and was combined in ratios with δ (for diameter or semidiameter) or ρ (for radius) to form circle constants.^{[97][98][99][100]} (Before then, mathematicians sometimes used letters such as c or p instead.^[101]) The first recorded use is Oughtred’s “0.Pi $\delta .\pi$ “, to express the ratio of periphery and diameter in the 1647 and later editions of Clavis Mathematicae.^[102][101] Barrow likewise used “Pi ${\textstyle {\frac {\pi }{\delta }}}$ ” to represent the constant 3.14…,^[103] while Gregory instead used “Pi ${\textstyle {\frac {\pi }{\rho }}}$ ” to represent 6.28… .^[104][99]

The earliest known use of the Greek letter π alone to represent the ratio of a circle’s circumference to its diameter was by Welsh mathematician William Jones in his 1706 work Synopsis Palmariorum Matheseos; or, a New Introduction to the Mathematics.^[3][105] The Greek letter appears on p. 243 in the phrase “12 ${\textstyle {\tfrac {1}{2}}}$ Periphery (π)”, calculated for a circle with radius one. However, Jones writes that his equations for π are from the “ready pen of the truly ingenious Mr. John Machin”, leading to speculation that Machin may have employed the Greek letter before Jones.^[101] Jones’ notation was not immediately adopted by other mathematicians, with the fraction notation still being used as late as 1767.^[97][106]

Euler started using the single-letter form beginning with his 1727 Essay Explaining the Properties of Air, though he used π = 6.28…, the ratio of periphery to radius, in this and some later writing.^[107][108] Euler first used π = 3.14… in his 1736 work Mechanica,^[109] and continued in his widely read 1748 work Introductio in analysin infinitorum (he wrote: “for the sake of brevity we will write this number as π; thus π is equal to half the circumference of a circle of radius 1″).^[110] Because Euler corresponded heavily with other mathematicians in Europe, the use of the Greek letter spread rapidly, and the practice was universally adopted thereafter in the Western world,^[101] though the definition still varied between 3.14… and 6.28… as late as 1761.^[111]

Modern Quest for More Digits

Computer Era and Iterative Algorithms

The development of computers in the mid-20th century again revolutionized the hunt for digits of π. Mathematicians John Wrench and Levi Smith reached 1,120 digits in 1949 using a desk calculator.^[112] Using an inverse tangent (arctan) infinite series, a team led by George Reitwiesner and John von Neumann that same year achieved 2,037 digits with a calculation that took 70 hours of computer time on the ENIAC computer.^[113][114] The record, always relying on an arctan series, was broken repeatedly (3089 digits in 1955,^[115] 7,480 digits in 1957; 10,000 digits in 1958; 100,000 digits in 1961) until 1 million digits were reached in 1973.^[113]

Two additional developments around 1980 once again accelerated the ability to compute π. First, the discovery of new iterative algorithms for computing π, which were much faster than the infinite series; and second, the invention of fast multiplication algorithms that could multiply large numbers very rapidly.^[116] Such algorithms are particularly important in modern π computations because most of the computer’s time is devoted to multiplication.^[117] They include the Karatsuba algorithm, Toom–Cook multiplication, and Fourier transform-based methods.^[118]

The iterative algorithms were independently published in 1975–1976 by physicist Eugene Salamin and scientist Richard Brent.^[119] These avoid reliance on infinite series. An iterative algorithm repeats a specific calculation, each iteration using the outputs from prior steps as its inputs, and produces a result in each step that converges to the desired value. The approach was actually invented over 160 years earlier by Carl Friedrich Gauss, in what is now termed the arithmetic–geometric mean method (AGM method) or Gauss–Legendre algorithm.^[119] As modified by Salamin and Brent, it is also referred to as the Brent–Salamin algorithm.

The iterative algorithms were widely used after 1980 because they are faster than infinite series algorithms: whereas infinite series typically increase the number of correct digits additively in successive terms, iterative algorithms generally multiply the number of correct digits at each step. For example, the Brent–Salamin algorithm doubles the number of digits in each iteration. In 1984, brothers John and Peter Borwein produced an iterative algorithm that quadruples the number of digits in each step; and in 1987, one that increases the number of digits five times in each step.^[120] Iterative methods were used by Japanese mathematician Yasumasa Kanada to set several records for computing π between 1995 and 2002.^[121] This rapid convergence comes at a price: the iterative algorithms require significantly more memory than infinite series.^[121]

Motives for Computing π

As mathematicians discovered new algorithms, and computers became available, the number of known decimal digits of π increased dramatically. The vertical scale is logarithmic. / Courtesy Wikimedia Commons

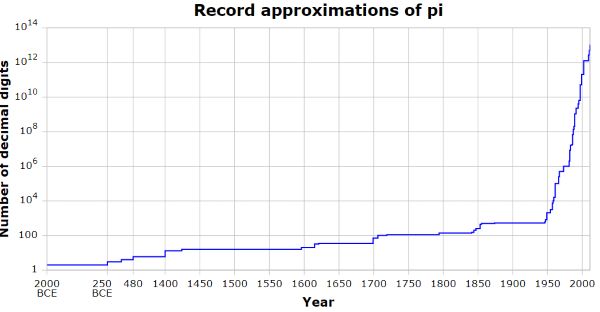
For most numerical calculations involving π, a handful of digits provide sufficient precision. According to Jörg Arndt and Christoph Haenel, thirty-nine digits are sufficient to perform most cosmological calculations, because that is the accuracy necessary to calculate the circumference of the observable universe with a precision of one atom. Accounting for additional digits needed to compensate for computational round-off errors, Arndt concludes that a few hundred digits would suffice for any scientific application. Despite this, people have worked strenuously to compute π to thousands and millions of digits.^[122] This effort may be partly ascribed to the human compulsion to break records, and such achievements with π often make headlines around the world.^[123][124] They also have practical benefits, such as testing supercomputers, testing numerical analysis algorithms (including high-precision multiplication algorithms); and within pure mathematics itself, providing data for evaluating the randomness of the digits of π.^[125]

Rapidly Convergent Series

**Srinivasa Ramanujan, working in isolation in India, produced many innovative series for computing π. / Courtesy Wikimedia Commons**

Modern π calculators do not use iterative algorithms exclusively. New infinite series were discovered in the 1980s and 1990s that are as fast as iterative algorithms, yet are simpler and less memory intensive.^[121] The fast iterative algorithms were anticipated in 1914, when Indian mathematician Srinivasa Ramanujan published dozens of innovative new formulae for π, remarkable for their elegance, mathematical depth and rapid convergence.^[126] One of his formulae, based on modular equations, is

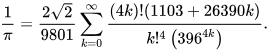
This series converges much more rapidly than most arctan series, including Machin’s formula.^[127] Bill Gosper was the first to use it for advances in the calculation of π, setting a record of 17 million digits in 1985.^[128] Ramanujan’s formulae anticipated the modern algorithms developed by the Borwein brothers (Jonathan and Peter) and the Chudnovsky brothers.^[129] The Chudnovsky formula developed in 1987 is

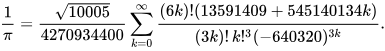
It produces about 14 digits of π per term^[130] and has been used for several record-setting π calculations, including the first to surpass 1 billion (10⁹) digits in 1989 by the Chudnovsky brothers, 10 trillion (10¹³) digits in 2011 by Alexander Yee and Shigeru Kondo,^[131] and 100 trillion digits by Emma Haruka Iwao in 2022.^[132] For similar formulae, see also the Ramanujan–Sato series.

In 2006, mathematician Simon Plouffe used the PSLQ integer relation algorithm^[133] to generate several new formulae for π, conforming to the following template:

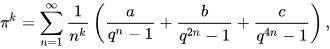
where q is e^π (Gelfond’s constant), k is an odd number, and a, b, c are certain rational numbers that Plouffe computed.^[134]

Monte Carlo Methods

**Buffon’s needle. Needles a and b are dropped randomly. / Courtesy Wikimedia Commons**

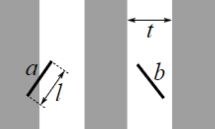
Monte Carlo methods, which evaluate the results of multiple random trials, can be used to create approximations of π.^[135] Buffon’s needle is one such technique: If a needle of length ℓ is dropped n times on a surface on which parallel lines are drawn t units apart, and if x of those times it comes to rest crossing a line (x > 0), then one may approximate π based on the counts:^[136]

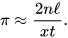
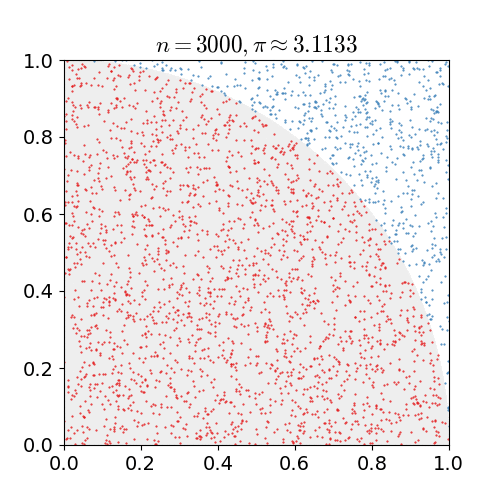
Another Monte Carlo method for computing π is to draw a circle inscribed in a square, and randomly place dots in the square. The ratio of dots inside the circle to the total number of dots will approximately equal π/4.^[137]

**Random dots are placed on a square and a circle inscribed inside. / Courtesy Wikimedia Commons**

Another way to calculate π using probability is to start with a random walk, generated by a sequence of (fair) coin tosses: independent random variables X_k such that X_k ∈ {−1,1} with equal probabilities. The associated random walk is

**Five random walks with 200 steps. The sample mean of |W₂₀₀| is μ = 56/5, and so 2(200)μ⁻² ≈ 3.19 is within 0.05 of π. / Courtesy Sławomir Biały, Wikimedia Commons**

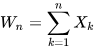
so that, for each n, W_n is drawn from a shifted and scaled binomial distribution. As n varies, W_n defines a (discrete) stochastic process. Then π can be calculated by^[138]

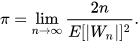
This Monte Carlo method is independent of any relation to circles, and is a consequence of the central limit theorem.

These Monte Carlo methods for approximating π are very slow compared to other methods, and do not provide any information on the exact number of digits that are obtained. Thus they are never used to approximate π when speed or accuracy is desired.^[139]

Spigot Algorithms

Two algorithms were discovered in 1995 that opened up new avenues of research into π. They are called spigot algorithms because, like water dripping from a spigot, they produce single digits of π that are not reused after they are calculated.^[140][141] This is in contrast to infinite series or iterative algorithms, which retain and use all intermediate digits until the final result is produced.^[140]

Mathematicians Stan Wagon and Stanley Rabinowitz produced a simple spigot algorithm in 1995.^{[141][142][143]} Its speed is comparable to arctan algorithms, but not as fast as iterative algorithms.^[142]

Another spigot algorithm, the BBP digit extraction algorithm, was discovered in 1995 by Simon Plouffe:^[144][145]

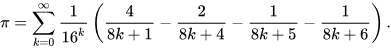
This formula, unlike others before it, can produce any individual hexadecimal digit of π without calculating all the preceding digits.^[144] Individual binary digits may be extracted from individual hexadecimal digits, and octal digits can be extracted from one or two hexadecimal digits. An important application of digit extraction algorithms is to validate new claims of record π computations: After a new record is claimed, the decimal result is converted to hexadecimal, and then a digit extraction algorithm is used to calculate several random hexadecimal digits near the end; if they match, this provides a measure of confidence that the entire computation is correct.^[131]

Between 1998 and 2000, the distributed computing project PiHex used Bellard’s formula (a modification of the BBP algorithm) to compute the quadrillionth (10¹⁵th) bit of π, which turned out to be 0.^[146] In September 2010, a Yahoo! employee used the company’s Hadoop application on one thousand computers over a 23-day period to compute 256 bits of π at the two-quadrillionth (2×10¹⁵th) bit, which also happens to be zero.^[147]

In 2022, Plouffe found a base-10 algorithm for calculating digits of π.^[148]

See endnotes and bibliography at source.

Originally published by Wikipedia, 11.11.2001, under a Creative Commons Attribution-ShareAlike 3.0 Unported license.

Matthew McIntosh

Administrator

Author's website Author's posts

Related Stories

Privileged by the Polis: Wealth, Access, and the Price of Citizenship in the Ancient World

Seen and Unseen: Surveillance, Migrant Mobility, and Control in the Medieval World

A History of Jewish Immigration and Labor Unions in the U.S. in the 19th and 20th Centuries