

Fourier recognized the possibility that the Earth’s atmosphere might act as an insulator of some kind.

Curated/Reviewed by Matthew A. McIntosh
Public Historian
Brewminate
Introduction
Jean-Baptiste Joseph Fourier[1] (March 1768 – 16 May 1830) was a French mathematician and physicist born in Auxerre and best known for initiating the investigation of Fourier series, which eventually developed into Fourier analysis and harmonic analysis, and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier’s law of conduction are also named in his honour. Fourier is also generally credited with the discovery of the greenhouse effect.[2]
Biography
Fourier was born in Auxerre (now in the Yonne département of France), the son of a tailor. He was orphaned at the age of nine. Fourier was recommended to the Bishop of Auxerre and, through this introduction, he was educated by the Benedictine Order of the Convent of St. Mark. The commissions in the scientific corps of the army were reserved for those of good birth, and being thus ineligible, he accepted a military lectureship on mathematics. He took a prominent part in his own district in promoting the French Revolution, serving on the local Revolutionary Committee. He was imprisoned briefly during the Terror but, in 1795, was appointed to the École Normale and subsequently succeeded Joseph-Louis Lagrange at the École Polytechnique.
Fourier accompanied Napoleon Bonaparte on his Egyptian expedition in 1798, as scientific adviser, and was appointed secretary of the Institut d’Égypte. Cut off from France by the British fleet, he organized the workshops on which the French army had to rely for their munitions of war. He also contributed several mathematical papers to the Egyptian Institute (also called the Cairo Institute) which Napoleon founded at Cairo, with a view of weakening British influence in the East. After the British victories and the capitulation of the French under General Menou in 1801, Fourier returned to France.

In 1801,[4] Napoleon appointed Fourier Prefect (Governor) of the Department of Isère in Grenoble, where he oversaw road construction and other projects. However, Fourier had previously returned home from the Napoleon expedition to Egypt to resume his academic post as professor at École Polytechnique when Napoleon decided otherwise in his remark
… the Prefect of the Department of Isère having recently died, I would like to express my confidence in citizen Fourier by appointing him to this place.[4]

Hence being faithful to Napoleon, he took the office of Prefect.[4] It was while at Grenoble that he began to experiment on the propagation of heat. He presented his paper On the Propagation of Heat in Solid Bodies to the Paris Institute on 21 December 1807. He also contributed to the monumental Description de l’Égypte.[5]
In 1822, Fourier succeeded Jean Baptiste Joseph Delambre as Permanent Secretary of the French Academy of Sciences. In 1830, he was elected a foreign member of the Royal Swedish Academy of Sciences.
Fourier never married.[6]
In 1830, his diminished health began to take its toll:
Fourier had already experienced, in Egypt and Grenoble, some attacks of aneurysm of the heart. At Paris, it was impossible to be mistaken with respect to the primary cause of the frequent suffocations which he experienced. A fall, however, which he sustained on the 4th of May 1830, while descending a flight of stairs, aggravated the malady to an extent beyond what could have been ever feared.[7]
Shortly after this event, he died in his bed on 16 May 1830.

Fourier was buried in the Père Lachaise Cemetery in Paris, a tomb decorated with an Egyptian motif to reflect his position as secretary of the Cairo Institute, and his collation of Description de l’Égypte. His name is one of the 72 names inscribed on the Eiffel Tower.
A bronze statue was erected in Auxerre in 1849, but it was melted down for armaments during World War II.[a] Joseph Fourier University in Grenoble was named after him.
‘The Analytic Theory of Heat’

In 1822, Fourier published his work on heat flow in Théorie analytique de la chaleur (The Analytical Theory of Heat),[8] in which he based his reasoning on Newton’s law of cooling, namely, that the flow of heat between two adjacent molecules is proportional to the extremely small difference of their temperatures. This book was translated,[9] with editorial ‘corrections’,[10] into English 56 years later by Freeman (1878).[11] The book was also edited, with many editorial corrections, by Darboux and republished in French in 1888.[10]
There were three important contributions in this work, one purely mathematical, two essentially physical. In mathematics, Fourier claimed that any function of a variable, whether continuous or discontinuous, can be expanded in a series of sines of multiples of the variable. Though this result is not correct without additional conditions, Fourier’s observation that some discontinuous functions are the sum of infinite series was a breakthrough. The question of determining when a Fourier series converges has been fundamental for centuries. Joseph-Louis Lagrange had given particular cases of this (false) theorem, and had implied that the method was general, but he had not pursued the subject. Peter Gustav Lejeune Dirichlet was the first to give a satisfactory demonstration of it with some restrictive conditions. This work provides the foundation for what is today known as the Fourier transform.
One important physical contribution in the book was the concept of dimensional homogeneity in equations; i.e. an equation can be formally correct only if the dimensions match on either side of the equality; Fourier made important contributions to dimensional analysis.[12] The other physical contribution was Fourier’s proposal of his partial differential equation for conductive diffusion of heat. This equation is now taught to every student of mathematical physics.
Real Roots of Polylnomials

Fourier left an unfinished work on determining and locating real roots of polynomials, which was edited by Claude-Louis Navier and published in 1831. This work contains much original matter—in particular, Fourier’s theorem on polynomial real roots, published in 1820. Fourier’s theorem on real roots of polynomials states that a polynomial with real coefficients has a real root between any two consecutive zeros of its derivative.[13][14]
François Budan, in 1807 and 1811, had published independently his theorem (also known by the name of Fourier), which is very close to Fourier’s theorem (each theorem is a corollary of the other). Fourier’s proof[13] is the one that was usually given, during 19th century, in textbooks on the theory of equations.[b] A complete solution of the problem was given in 1829 by Jacques Charles François Sturm.[15]
Discovery of the Greenhouse Effect
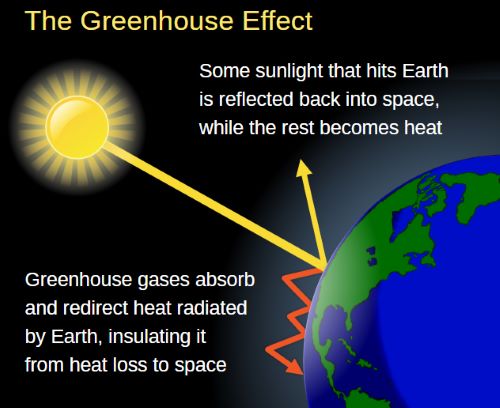
In the 1820s, Fourier calculated that an object the size of the Earth, and at its distance from the Sun, should be considerably colder than the planet actually is if warmed by only the effects of incoming solar radiation. He examined various possible sources of the additional observed heat in articles published in 1824[16] and 1827.[17] However, in the end, because of the large 33-degree difference between his calculations and observations, Fourier mistakenly believed that there is a significant contribution of radiation from interstellar space. Still, Fourier’s consideration of the possibility that the Earth’s atmosphere might act as an insulator of some kind is widely recognized as the first proposal of what is now known as the greenhouse effect,[18] although Fourier never called it that.[19][20]
In his articles, Fourier referred to an experiment by de Saussure, who lined a vase with blackened cork. Into the cork, he inserted several panes of transparent glass, separated by intervals of air. Midday sunlight was allowed to enter at the top of the vase through the glass panes. The temperature became more elevated in the more interior compartments of this device. Fourier noted that if gases in the atmosphere could form a stable barrier like the glass panes they would have a similar effect on planetary temperatures.[17] This conclusion may have contributed to the later use of the metaphor of the “greenhouse effect” to refer to the processes that determine atmospheric temperatures.[21] Fourier noted that the actual mechanisms that determine the temperatures of the atmosphere included convection, which was not present in de Saussure’s experimental device.
See endnotes and bibliography at source.
Originally published by Wikipedia, 10.03.2002, under a Creative Commons Attribution-ShareAlike 3.0 Unported license.


