

By Dr. Taylor McCall
Associate Editor
Speculum: A Journal of Medieval Studies
Introduction
The idea of science in the early Middle Ages is a broad one that encompasses many subjects. To understand this, we should think of the root of the word ‘science’, which comes from the Latin term scientia, meaning ‘knowledge’. In the Middle Ages, a person’s ‘science’ referred to his understanding of a particular topic. Our modern concept of science as a field—comprising subjects like biology and chemistry—is a much narrower definition than what our medieval predecessors comprehended.
In fact, we oftentimes today associate science with secular: facts one can observe in nature, allowing little room for the divine. The Christian West saw no such divisions; indeed, God was understood to have created everything for a specific purpose, and man could only attempt to discover the complexities of creation.
Early Medieval Learning and the Quadrivium

Following the fall of Rome in the fifth century, the classical knowledge that served as the foundation of Roman learning was, for the most part, lost to Western Europe. Many of the most celebrated geniuses of the classical past—including Aristotle, Plato, and Euclid—wrote in Greek, and the Greek language quickly fell into disuse. While some treatises were translated into Latin and circulated in Western Europe, the vast majority of classical learning remained in the eastern parts of the former Roman Empire and the Middle East.
Several learned men were responsible for the preservation of at least some classical learning in medieval Europe. Boethius (b. c. 470, d. 524), a Roman politician who is perhaps best known for his philosophical works, wrote and translated Greco-Roman texts on the quadrivium: the four subjects of arithmetic, geometry, astronomy and music. The quadrivium was taught after the preparatory trivium, which comprised the three subjects of grammar, logic and rhetoric. Together, they formed the seven liberal arts and acted as the bedrock of medieval education, first in monasteries and cathedral schools, and then when universities were established in the 12th century. Boethius is thought to have coined the term quadrivium in his writings, and his treatise on arithmetic was widely circulated in the early Middle Ages.
After the sixth century, quadrivium learning was mostly confined to monasteries and cathedral schools, and the pursuance of scientific queries—from the study of natural phenomena to mathematical equations—was largely overshadowed by theological concerns. Monks educated themselves in practical sciences like medicine and architecture to heal their sick and build their churches, studied astronomy to determine times for prayers, and used arithmetic for the everyday running of their accounts.
Calculating Moveable Feasts
Among the earliest and most widespread mathematical texts and diagrams are those that dealt with computing the date of Easter, which involved using both arithmetic and astronomy. Determining the date—which is ambiguous in the Bible but close to the Jewish celebration of Passover—occupied many early theologians for centuries. It was acknowledged that Easter should always fall on a Sunday generally near Passover, and eventually, the Western church agreed it should be celebrated the Sunday after the 14th day of the Paschal (or Easter) month, determined as the month in which the 14th day is on or after the vernal (or spring) equinox. However, this opened another can of worms; there was no exact consensus between the various branches of Christianity on how to determine the vernal equinox. Eventually, the Western Church adopted the Alexandrine method of computing the date of Easter, which would remain in effect until the Gregorian calendar reform of 1582.
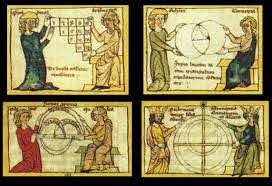
Computus tables, charts used in determining calendar dates of Easter and other moveable feasts (many of which were tied to lunar and solar cycles), were common in early Insular and Continental manuscripts. A fragment collection of theological treatises made in both England and France in the 11th and 12th centuries (now BnF, Latin 15170), includes a wonderfully dynamic full-page drawing of a teacher instructing a group of students on computing.

The scene takes place beneath two archways, above which are drawn a cluster of towers. The instructor is seated on the left in a large chair, his students before him. He holds a gilded disc divided into three sections resembling T-O map, right finger raised as he lectures. One of his students, who is standing in the background, counts upon his fingers; the two seated before him hold a writing tablet and stylus and a folded piece of parchment, respectively. The image is followed by a calendar and many multicoloured computus diagrams, some decorated with architectural elements.
Computus Diagrams
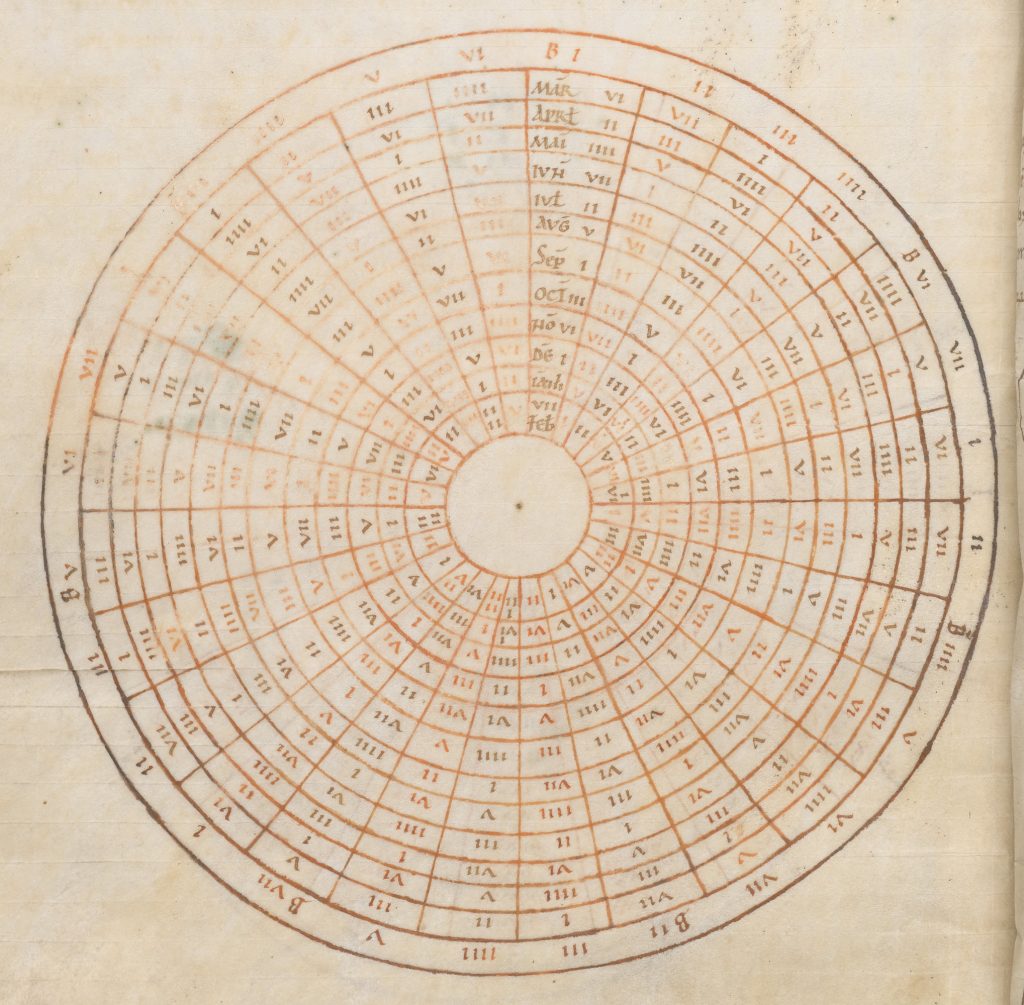
An example of an early computus diagram is found in a collection of works made in Lyon in the 11th century (British Library, Sloane MS 263). The manuscript contains computus diagrams and includes texts by two important early figures in scientific learning, Helperic of Auxerre (fl. c. 900) and the English Benedictine monk Bede (b. c. 673, d. 735). Helperic was a Benedictine monk who was educated at the Abbey of Saint-Germain d’Auxerre in modern-day central France. He produced one of the most popular works on computus of the Middle Ages, De computo (On the Computus). Known as the ‘Venerable’, Bede wrote extensively on historical and theological topics, and he also tackled the controversial topic of the correct way to compute the date of Easter. His texts are often included with computus tables.
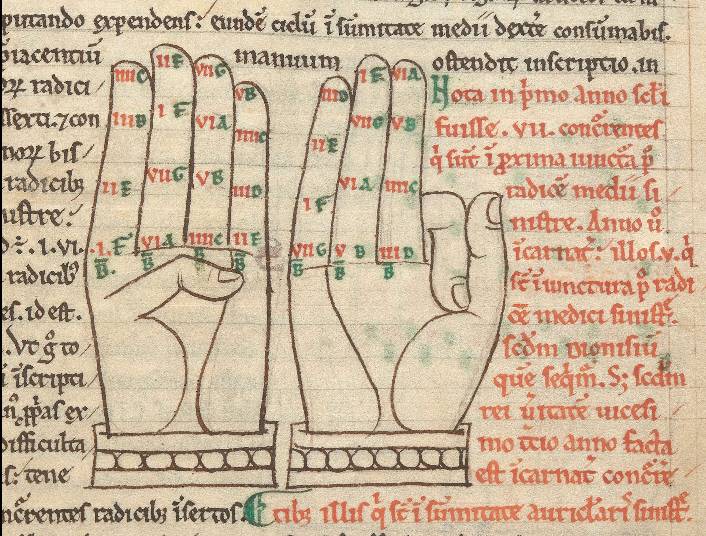
Extensive computistic diagrams and tables feature in a later English compendium of computus and astronomical works (British Library, Egerton MS 3314). Created in Canterbury in the 11th or 12th century, this manuscript collection demonstrates the continued importance of the science of computation and relevance of Bede’s work, as well as the power of diagrams in translating difficult and complicated ideas into simple schematics. The manuscript also reveals how to do mathematical calculations and compute Easter dates by hand. Full hands are presented and divided into sections labelled with figures, demonstrating finger-counting. Computational treatises and diagrams continued to be copied well into the 16th century.
Mathematics
Up until the 12th century, the most advanced mathematics in Western Europe were computistic in nature. Much of the heritage of ancient Greece—including Euclid’s Elements—was unknown to Western Europe until the 12th century, which saw Latin translations of Greek and Arabic texts imported into Europe. Rudimentary arithmetic and geometry were taught in monasteries and monastery schools, but there was little original contribution to either field until new treatises began to filter into Europe from the Middle East.

A good representation of pre-12th century mathematics is a copy of Boethius’s De institutione arithmetica (On Arithmetic) made in the mid-11th century (BnF, Latin 10251). The manuscript was made potentially in Dijon, and is filled with mathematical diagrams throughout.

A later version of the same text can be found in a copy of Boethius’s work on arithmetic made in England or France in the third quarter of the 12th century (British Library, Harley MS 549). This manuscript also contains mathematical diagrams, and in particular, a colourful, highly decorated multiplication table for Roman numerals.
Astronomy
The educational reforms instigated by Charlemagne during the Carolingian Renaissance in the late 8th and early 9th centuries in France revitalised the study of astronomy, and ensured it was taught in monastic schools across the Empire. Advances in astronomy flourished in the Middle East during the period, and astronomical knowledge was considered paramount to learned men in the West. For example, the 11th century saw the introduction of the astrolabe into Europe from the Middle East. An astrolabe was a device used to measure the position of the planets and in making astrological predictions. Such predictions were especially critical for medical practitioners, who relied on the positions of the planets and zodiac—believed to be linked to distinct parts of the body—to determine the best and worst times for bloodletting and other procedures. Students in universities beginning in the 12th centuries studied astronomy—alongside arithmetic and geometry—as part of their quadrivium curriculum, and slow progress in all three disciplines began to be made.
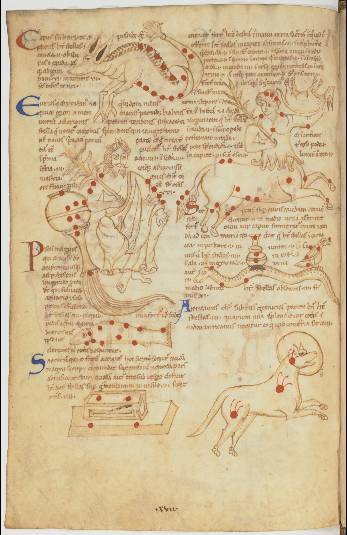
The astronomical images and texts that survive to today are sometimes instantly recognizable and sometimes confusingly obscure to the modern viewer. The orbits of the planets are often depicted as many circles nested together. An astronomical collection produced during the second and third quarters of the 12th century in France (possibly Chartres), contains many neatly measured planetary diagrams of concentric circles (ff. 203-228v), as well as several striking images of the constellations and zodiac figures (ff. 229v-232v) (BnF, Latin 14754). Further, a miscellany of computistical and astrological texts created between 1075-1222 in northern or central France (British Library, Royal MS 13 A XI), charts the orbits of the various planets onto a graph (f. 143v).
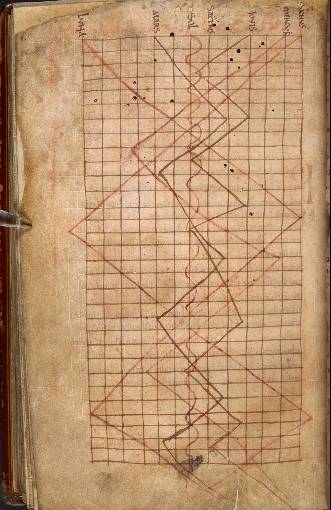
The manuscripts we have discussed here represent a very small portion of pre-1200 scientific manuscripts. However, they offer a vivid glimpse of the ways in which men understood the natural world before the influx of new texts into Western Europe forever altered scientific knowledge.
Originally published by the British Library under the terms of a Creative Commons Attribution 4.0 International license.


