The 'Prehistory' of the Philosophy of Science

*The School of Athens*, by Raphael / Courtesy Vatican Museums, Wikimedia Commons

Differences between our understanding of the concept of ‘science’ and that of more ancient philosophers.

By Dr. Jesús Zamora Bonilla
Professor of Logic and Philosophy of Science
Dean, Faculty of Philosophy
Universidad Nacional de Educación a Distancia (UNED)

By Way of Introduction

Since this will be a series of entries about something as weird as the ‘prehistory’ of philosophy of science, I think readers deserve a little explanation about what I do exactly mean by that. ‘Philosophy of science’, to begin with, is a topic that took its current status as an autonomous academic field (I mean, something about which you may hold a university chair, or found a journal exclusively devoted to it) around the beginning of the 20^th century, with the ‘Vienna Circle’ of Schlick, Carnap, Neurath, etc., and their journal Erkenntnis, being their official ‘founding event’ in most mythographies. Obviously, neither were these intellectuals creating a new branch of reflection ex nihilo, nor had philosophers since the beginning of the times abstained from thinking, very deeply indeed, on topics related to ‘science’. Actually, reflection about what science is and how can we got it was what for most of those oldie philosophers philosophy was mainly about.

Current academic practice, however, tends to follow an institutional division of labour according to which most of the discussion about ‘science’ ante 1900 belonged to a different intellectual field known as ‘epistemology’ (or ‘theory of knowledge’, in spite of the Greek word epistéme meaning, precisely, science, and having been always translated into Latin as scientia). This has had the disappointing result that current ‘epistemologists’ (especially in the analytic tradition) tend to focus on cases of ‘knowledge’ whose prototypical examples would be things like ‘John knows that there are some beers in the fridge’ (something that Plato would have been horrified by someone taking it as a case of epistéme), instead of things like, say, ‘we know that matter is composed of atoms’. So, these epistemologists have nearly nothing to say about the questions philosophers of science tend to ask, a situation that is sadly parallel to the lack of interest of most philosophers of science about discussions on epistemology. (By the way, in the French philosophical world, as a proof of greater etymological bon sens, the word épistémologie has been more usually preserved to refer to what other countries called ‘philosophy of science’).

**Karl Popper in the 1980s. / Courtesy LSE Library, Wikimedia Commons**

I will not attempt here to fight against the windmill of this schizophrenic situation (though some items of schizophrenic philosophy are going be prominent case studies in my series), but will remain deferentially compliant to the custom of considering philosophy of science as an enquiry about scientific knowledge in the contemporary sense of ‘scientific’, and hence, giving more relevance (in the expression in italics) to the ‘scientific’ than to the ‘knowledge’ half. So, my ‘prehistory of philosophy of science’ will basically consist in recounting what pre-contemporary philosophers would have to say about what we (not them) understand by ‘science’. My introduction demands to start, hence, by explaining the main differences between our understanding of the concept of ‘science’ and that of more ancient philosophers.

To begin with, we tend to automatically identify the word ‘science, first and foremost, with a kind of reality that consists in a social activity, an important element in our social fabric, institutionalised in the system of universities, research centres, libraries, publishers, congresses and seminars, school curricula, documentaries, and, of course, in the corpus of items of ‘knowledge’ this system helps to create, consolidate and transmit. After all, scientists, the people who do science, are, as different from ‘natural philosophers’, or from ‘philosophers’ tout court, a creation of the 19^th century, the term being coined by the author who will be one of the last protagonists of our saga: William Whewell (1794-1866).

Of course, it is not that ancient philosophers simply ignored the ‘social flesh’ that was necessary to enjoy something like ‘science’: Aristotle famously -and delightedly- pondered about slavery as a necessary precondition for the existence of a happy class of wealthy, bearded people having plenty of free time (skholé in Greek, otium in Latin) to devote themselves to advanced learning. But their main philosophical concern was about the (purely intellectual) ‘nature’ of knowledge, rather than about its (social or economic) ‘nurture’, so to say. You can justly respond by pointing out that most of the ‘orthodox tradition’ in contemporary philosophy of science, from Carnap and Popper to Bas van Fraasen or Stathis Psillos, barely spend a paragraph talking about the social flesh of science (though it has been much less so in the last fifty years), but my point is not that we should identify philosophy of science with sociology of science, or something like that: I am simply telling that the object of contemporary philosophy of science, in contraposition to the object of classical epistemology, is now immediately recognised as an essentially social construction (not in the sense that it is a ‘mere’ social construction: sport is also a ‘social construction’ but that does not make of myself a tennis player as proficient as Roger Federer), rather than as something belonging to the realm of the abstract, individual mind. Even if philosophy of science (or ‘methodology’, as it is also often named) tries essentially to answer the question of ‘how to attain knowledge’, the subject of that question, the one being responsible for attaining that knowledge, is naturally seen nowadays as ‘society’, or at least as a ‘social institution’, and not as a monadic Robinson Crusoe. By the way, we already saw in this blog how Popper himself understood this.

In the second place, contemporary philosophy of science is not as obsessed (or it is not obsessed at all) as pre-contemporary philosophy was about whether scientific knowledge is ‘indubitably certain’. Actually, after Popper’s critique of verificationism, and also under the long shadow of Hume’s critique of induction, science is not usually understood (at least amongst philosophers, and usually by most scientists; since more recent times, not by a large part of the general public either) as knowledge that has been proved beyond any possible doubt. Most scientific theories and laws are seen, instead, as idealised, simplified, approximate and provisional models, always subject to improvement, if not blatantly conjectural and faute de mieux in many cases. This leads to a funny contrast between our science and the science of the times of Aristotle or Kant: we recognise the falibility and imperfectness of our scientific knowledge much more than they did with theirs, in spite of our knowing that our scientific knowledge is vastly better than theirs in basically all respects.

Lastly, and directly connected to the previous two points, we are unavoidably conscious of the colossal complexity of science, both in terms of the ‘internal’ relations between each item of knowledge and a myriad of other items, and of the ‘external’ connections between the epistemic and the practical (relations and connections that can be positive or adverse), whereas classic philosophers tended to reserve the label epistéme to the ‘purest’, most ‘intuitive’, less ‘contaminated’ forms of intellectual wisdom, the less poluted with ‘practical’ or ‘wordly’ junk, the better. We know science is less a pyramid than a mangle, to use Andrew Pickering’s metaphor.

Hence, what will this ‘prehistory of philosophy of science’ be about? In a nutshell, may aim is to illustrate how the evolution of our contemporary understanding of science can be traced through the works of some authors prior to the last hundred years, i.e., how some of their ideas can be regarded as ‘philosophy of science avant la lettre’ (even if, of course, I shall yield at times to the temptation of refashioning them a little bit, in order to make the story more lively). We shall start, of course, by the very beginning, with the oldest preserved document that can be rightly considered as a work on ‘philosophy of science’. A document that, obviously, was written by a Greek, more than two millenia ago.

Is There a Doctor on Board?

**A mosaic of Hippocrates on the floor of the Asclepieion of Kos, with Asklepius in the middle, 2nd-3rd century. / Courtesy Wikimedia Commons**

In the previous section I devoted to something that we might call ‘the problem of scientific method’ was written by Democritus (around 460-370 BC), the author the philosophical systems of Plato and Aristotle were constructed against, and whose ideas were so revolutionary that it seems that nobody in the last centuries of the Ancient times worried about preserving a copy of his more than seventy books, for none of them survived till the Middle Ages. Perhaps the treatises called On the Foreknowledge of the Future, or On the Criterion of Thought, mentioned in the catalogue described in Diogenes Laertius Lives of the Philosophers, contained some more detailed ideas about how to carry out research than what the clumsy references by Aristotle and later authors on the topic (Plato never debased himself to mentioning Democritus explicitly) allows us to glimpse. But it is also possible that Democritus’ understanding of how to gain knowledge was too naive for the radicality of his Weltanschaaung, so that his naivety helps to explain in part the reluctance to accept his strange views about Nature and Man. Hence, we cannot presume that the father of atomism, besides being a prominent philosopher and an accomplished mathematician himself (he was the first to prove the formula for calculating the volume of a pyramid and a cone, sowing the first seeds of what many centuries later would become the infinitesimal calculus), was also a captivating proto-philosopher of science, and so he will not be, unfortunately, the real protagonist of this first chapter of my story.

The honour of being the first ‘book’ (actually, a very short treatise, not even twenty pages long; it’s a ‘book’ in the archaic sense of being a work fitting within a roll of papyrus, or biblion) that we can consider a philosophy-of-science forerunner corresponds to an anonymous pamphlet that today we wouldn’t even consider a ‘philosophical’ work, but rather a piece of sheer propaganda or blatant advertising. The date of the work is a little bit less uncertain, and very probably it is contemporary of the mature Democritus, around the last third of the 5^th century BC, also the time of Socrates’ flowering, and also of the great ‘sophists’ Protagoras, Gorgias and Hippias, to which it is much more closely related by its style, structure and content. It has been preserved within the so called Hippocratic Corpus, a collection of around sixty short medical treatises attributed to the ‘father of medicine’, Hippocrates of Kos (also contemporary of the aforementioned intellectuals), but that most likely were, most of them (including ours), composed by his followers during the last decades of the 5^th century and the first ones of the 4^th. The succinct title with which the book has gone down in history is On the art (Perì téchnēs), though frequently it is also published or referred to as On science, for the Greek word téchnē had a wide meaning that covered all types of practical knowledge, from the most rustic craftsmanships to more illustrious skills like architecture, navigation, military engineering, and of course what we call the ‘fine arts’ (sculpture, painting, music…). In this case, of course, the téchnē that is the object of discussion is the profession of medicine, and actually the booklet’s title is some times translated as On medical science.

The question debated by the anonymous author is whether medicine can count as a science (or ‘art’), or not, and obviously the answer of the book is given in the affirmative. The work has the unmistakable flavour of sophist debates, so much that one almost imagines the existence of a lost, parallel treatise of equal length, in which the opposite conclusion was reached. Sophists, after all, were famous by the talent of being able of persuading their audiences both of any thesis and of its contrary. Actually, many of the arguments of Perì téchnēs are so obviously flawed (at least for us, fortunate enough to having known a medical science hugely more powerful than its ancient counterpart), that we cannot resist the feeling of its sophistry. The criticisms to medical science the author tries to counteract are the following (as I have said, it’s easy to imagine a previous chapter in which these theses were defended):

Patients that heal recover by chance, not by the effect of the medical treatment.
Many sick people recover without consulting the physician.
Some patients die in spite of being treated.
Physicians reject to treat incurable patients.

**An 18th-century engraving of Galen by Georg P. Busch. / Courtesy Wikimedia Commons**

The last objection is probably the one that is more easily responded by the author: no art/science has an infinite power, and all have limits that are fixed by nature; only ignorants could demand that medicine can heal every sickness, for, are not all men mortal, after all? Knowing in which cases the illness is going to be more powerful than the instruments of the physician is, then, not a sign of lack of learning, but of wisdom. However, the answer provided is in a way too easy, as it is clear from the fact that it sounds so bizarre to us that Hippocratic doctors just refused to treat patients that were too sick. The progression of an illness is usually not ‘deterministic’ (as we would say), but often very unpredictable, and hence we are amazed by the fact that those physicians were not more inclined to trying different therapies in the hope that some might work, at least in a few cases. Of course, it is also possible that the professional behaviour of those physicians were not, in practice, as ruthless with the seemingly incurable as the letter of the text suggests, and in fact, many specialist think that the author was probably not a doctor himself, and was more interested in the sophistical debate than in precisely reporting the practice of medicine.

The other three points are more interesting, though the answers are rather disappointing. We, moderns, would expect an argument in the style of a proto-statistical analysis of the effectiveness of being treated against that of not-being treated, something like the suggestion that the chance of recovering is higher when the patient is treated by a doctor than when it is not (have you not thought of something like that when reading points 1 to 3?). Nonetheless, we find nothing like that. It even seems that the author tacitly acknowledges that the chance of being healed by a doctor is actually not higher than that of recovering spontaneously. For the answers he offers (I am obviously assuming the author was a man, though we cannot know for sure) are of the following style:

“I do not exclude the operations of Fortune, but I think that those who receive bad attention usually have bad luck, and those who have good attention good luck. (For) what else but medical skill can be responsible for the cures of patients when they have received medical attention? (…) (The patients) didn’t want to trust in the shadowy form of Fortune, but in the art of medicine, (and so) the share of chance is excluded, but that of art is not.

(…) No one who is cured without the services of a doctor can ascribe his cure to chance. Indeed, upon examination, the reality of chance disappears: Every phenomenon will be found to have some cause, and if it has a cause, chance can be no more than an empty name”.

And, as for the patients that recover without the intervention of a doctor:

“Should they be cured, it is because they have employed the same remedy as a doctor would use. And this is a considerable demonstration of the reality and the greatness of the medical art, when we realize that even those who do not believe in it are nevertheless saved by it”.

Lastly, about the patients that do not heal, in spite of the physician’s efforts, the answer is still funnier’:

“It is fare more likely that the sick are unable to carry out the instructions than that the doctors prescribe the wrong remedies. Physicians come to a case in full health of body and mind, and compare the present symptoms of the patient with similar cases they have seen in the past, so that they can say how cures were effected then. But the patients do not know what they are suffering from, nor why, nor what will succeed, nor have they experience of similar cases. Their present pains are increased by fears for the future. They are full of disease and starved; they prefer an immediate alleviation of pain to a remedy that will return them to health. Such is their condition when they receive the physician (…) Is it not more likely that they will disobey their doctors rather than that the doctors (…) will prescribe the wrong remedies?”

In a nutshell, what the author of On the art is telling us is that:

When medicine intervenes, there is no place to chance.
When a patient heals without the help of a doctor, it is because by accident he or she had done what the doctor would have prescribed nevertheless.
When a patient does not heal in spite of being treated by a doctor, it is because he has not followed the physician’s prescription.

As you see, these arguments would be more reasonably found nowadays within a lawyer’s plea of defence in a trial against a physician’s malpractice than in a methodological essay on medical procedures. I’m sorry that, perhaps, if you were waiting for a deeper example of ancient wisdom about ‘what science consists in’, you are a little bit disappointed with the first author I have examined in this series. Don’t blame him too much, after all, as I said, it was probably the first attempt of jotting down some systematic ideas about the working of the sciences (or the ‘arts’), and we can be sure that the implicit knowledge of their practitioners about this question was substantially more advanced than the awkward answers our anonymous sophist was able of assembling. I will just finish mentioning the two ideas the author of this book got definitely right:

First, medical science is not a matter of superstition or religion (no single reference to gods appears in the book, if we discount the mention of Fortune, which is discarded), but of experience and nothing but experience (“there is no science that is not based on facts”).

Second, medical science is far from perfect, and we should always keep on researching in order to make more and more new discoveries.

Introducing Plato

**Roman copy of a portrait bust of Plato, c. 370 BC. / Courtesy Capitoline Museums, Wikimedia Commons**

If the preceding section turned out being a little bit disappointing because of the clumsiness and sophistry of the anonymous author of the leaflet we know as On the (medical) science (the first preserved complete work which discusses the nature of a ‘science’, or, in this case, téchnē), we reach today an immensely more gifted and judicious writer, probably one generation younger, and that happens to be the first philosopher from whom complete books have survived: even a lot of books, around thirty, some of them rather thick. I’m talking, of course, of no other than the great Plato (427-347 BC). By the way, the name ‘Plato’ means literally ‘Big-boned’, and it seems to have been his nickname as a wrestler when he was young, his true name being probably ‘Aristocles’. Plato was really a big figure.

Independently of the sympathies or antipathies that you may feel for Plato’s views, the undeniable truth is that Plato is one of the very, very few people (five? ten?) deserving to be considered as true pillars of civilisation. The thought of the previous ‘philosophers’ seems a mere oracular babbling, whereas in Plato’s texts we find the real light, the highest clarity and detail of philosophical arguments, and we find it in a literary form he expressly created, the ‘dialogue’, where flesh-and-blood people talk to each other, and to us, with all the freshness of an amicable conversation. It’s not strange that the Platonic dialogues were copied and recopied, read and devoured so many times during the Antiquity and the Middle Ages, that his written work was preserved more safely than that of any other Greek author. Plato established basically all the areas of what we understand as ‘philosophy’, from ethics to metaphysics, from philosophy of language to politics, from aesthetics to anthropology; perhaps the only big exception is that of formal logic, established by his direct disciple, Aristotle, but as a kind of clarification of what Plato called ‘the art of dialectics’. Of course, epistemology as an explicit branch of philosophical reflection was also inaugurated by Plato, on top of the careless attempts of a fistful of myopic predecessors like the ones we mentioned in the preceding entry.

Before entering into Plato’s ‘philosophy of science’ (epistēmē), it is necessary to recall that his relation to science goes much beyond his own writings, for the Academy he founded served as the most-powerful-to-date centre of research in the ancient world, so much that it is justified to take it as the ‘first university’ in history. In particular, mathematics, astronomy and musical theory are fields in which great advances were made by people working at some moment in the Academy, like Theaetetus, Archytas, Eudoxus and Eudemus. Aristotle himself studied and taught there during the last twenty years of Plato’s life, though his biological work, which we shall consider later in this series, was mainly done after that time. So, Plato had a great concern for ‘the sciences’ (to which he usually refers as tekhnái, or ‘arts’), and promoted a considerable progress in scientific knowledge, the biggest one before the founding, almost one century later, of the ‘Library’ in Alexandria, even if, besides his theories about physics and cosmology that will appear in our next entry, he made little specific contributions to them. In this sense, Plato’s contribution to our understanding of science also has to include the intuition that the most natural and efficient environment for the growth of scientific knowledge is something like what we know today as research centres and scientific communities. He also inagurated the idea that these centres and communities should be supported by the state (though his own Academy wasn’t, but this is the claim we can derive from the description of the ideal state he offers in The Republic), and open to people from different social backgrounds… and even women!, for at least two female members of the Academy are known, Axiothea of Phlius and Lasthenia of Mantinea.

As for Plato’s specific view of the nature of science and knowledge, probably the best explanation he offers is also in The Republic, at the end of book VI, just in the previous paragraphs to those in which (at the beginning of book VII) he presents his definitely more famous ‘myth of the Cave’, of which nothing will be said here. The section I am referring to is known as ‘the simile of the line’, and in it Plato introduces his hierarchical model of ‘degrees of knowledge’. We, the moderns, tend to interpret this expression as referring mainly to differences in the “amount of certainty” each particular theory, proposition or hypothesis has. But Plato’s opinion is rather different. Basically, his claim is that differences among the types of ‘knowledge’ (the difference that there is between a mathematician proving a theorem, and a pair of rascals gossiping in the shadow of the Athenian agora, say) correspond essentially to differences in the types of entities those items of knowledge are about. In a nutshell: ‘better’ kinds of knowledge are ‘better’ because they deal about ‘better’ things. Of course, the ‘higher’ types of knowledge also provide more certainty, but this is secondary, only an accidental sign of the essentially different nature of the things known. The question is, hence, what are these ‘things’? Plato’s answer is given through a visual model, that we are reproducing here.

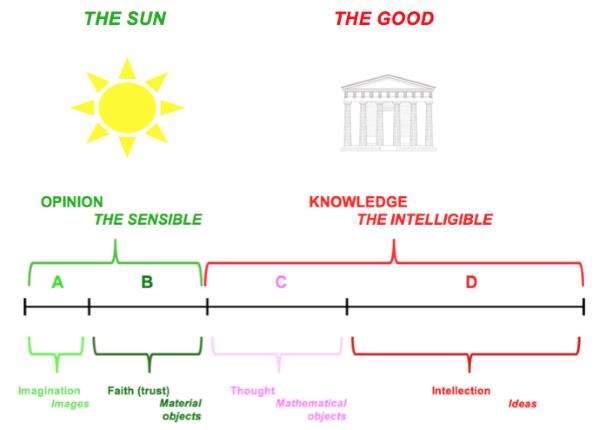
Socrates (the character that in The Republic is explaining this theory to another persona named Glaucon, that in the real world was, equally as Adeimantus, another of the conversants in the dialogue, one of Plato’s elder brothers) invites us to take a line ABCD, and divide it into two unequal segments, AB and CD. One of these corresponds to ‘the sensible things’, those that we can perceive by our senses (more importantly, sight); the other segment corresponds to ‘the intelligible things’, those that cannot be seen, but only thought about (curiously, the text does not decide whether the ‘big’ part is the one that correspond to the intelligible, or it is the small one, but tradition has opted for the representation chosen here). Besides the way in which we perceive or ‘catch’ those different types of entities, another essential difference is that the sensible things are subject to change, whereas the intelligible things are not: they are ‘eternal’. Hence, ‘knowledge’ of mutable, sensible things is what Plato calls opinion (dóxa), whereas that of intelligibles is… well… real knowledge (gnosis), or as we would say, scientific.

Before discussing what those ‘intelligibles’ can be, let’s pause to analyse the next move in Socrates explanation: each segment of the full line must be divided again according to the same proportion. Hence, the segment of the sensible things is divided into two sub-segments, A and B, such that the ratio of A to B is the same as the ratio of AB to CD. This is a metaphor to indicate that the relation between the sensible (AB) and the intelligible (CD) is analogous to the relation between the two kinds of entities that belong to the sensible realm, and which according to Socrates… sorry, to Plato… are the material things B (prágmata) and the images A (éikones, like those in mirrors, calm water, pictures, etc.). This has to be interpreted, obviously, as meaning that the sensible things are a kind of ‘images’ or ‘copies’ of intelligible things, something to which we shall return immediately. Before that, I have just to indicate that, as in the case of the to bigger segments, here there are also two hierarchical different kinds of ‘knowledge’ related to the two types of entities or the two types of ‘epistemic achieving’: to images it corresponds imagination (eikasía), whereas to material things it corresponds faith (pistis), which, in Plato’s times, is ‘faith’ not in the religious sense of ‘believing in the miraculous’, later associated to the spread of Christianism, but in the wider sense of ‘trusting without an absolute proof’, or ‘pragmatic belief’ (we are talking about prágmata, after all). This pistis is perhaps more similar to what some philosophers of science known as ‘the natural ontological attitude (NOA)’, that of accepting acritically the existence of the things surrounding us, or to the ‘Lebenswelt’ or ‘being-in-the-world’ of phenomenologists like Husserl or Heidegger.

The moral of all this is that, according to Plato, there is no science of the material things, only ‘opinion’, opinion that, in the best of the cases, is something that we trust, but acritically, without sufficient reason. After all, imagination (of which dreams would be a paradigmatic example) is, more clearly still, not ‘science’ or ‘knowledge’ at all. What Plato is telling us is, hence, that ordinary knowledge of the material world is just a kind of ‘dream’, or, more precisely, that it is to real science no more than what dreams are to wakefulness.

‘Socrates’ proceeds then to divide the other segment of the line according to the same proportion, so that C is to D as A is to B (or as AB is to CD). C corresponds to mathematical entities (the examples mentioned by Plato are actually geometrical entities: the circles, lines, etc., mathematical theorems speak about; he does not mention numbers, what may lead us to ponder whether he would have placed these into C or into D). Lastly, the inhabitants of D are… you correctly guessed it: what we know as ‘Platonic Forms’ (éidē, singular éidos), or what in most other languages than English are known as ‘Platonic ideas’ (éidos means literally the ‘aspect’ or ‘(visual) shape’ of something, and comes from the same Indo-European root as latin video, ‘I see’; idea also derives from éidos, with basically the same meaning in Greek). ‘Form’, in Greek morphē, is probably a translation Plato himself wouldn’t have approved, though, as you know, was the term of choice for Aristotle to describe something similar, that we shall encounter later in this series. In fact, there is a deep reason for rejecting that translation, one that is easy to see when we examine the relation between C and D: mathematical objects like triangles, the inhabitants of C, have, obviously, a spatial form, a shape, but D, the highest realm, does not contain ‘triangleS’, but, instead, it contains the essence of triangularity, that in which being a triangle consists, what we think about (but do not see) when we think about a figure that it is a triangle. This essence is the ‘Form’ of triangle, but not in the sense of having this geometrical form (an equilateral one, say), or that form (a scalene triangle, for example), but in the sense the most abstract and universal definition or understanding of triangularity.

So, if C is to D as A is to B, this means that specific triangles are also like copies of ‘the Triangularity’, and this also means that the kind of knowledge that we might attain of mathematical entities is not as ‘pure’ as the knowledge we may have of the Forms: ‘thought’ (‘discursive thought’, or ‘thinking step-by-step’, would be better translations of diánoia) is like a kind of ‘dream’ as compared to ‘intellection’ (nóesis). Probably because of this, Plato refers to the ‘sciences’ belonging to the segment C as tékhnai, ‘arts’: mathematics, astronomy and music (the two last ones not being ‘empirical’ astronomy and music, but their ‘theoretical’ counterparts, a topic to which we shall return in the next entry). The only real science (epistēmē) mentioned in the relevant paragraphs of The Republic is what he calls ‘dialectics’, or ‘the dialectical science’ (dialektikē epistēmē), which is a curious name for a science, of course: ‘dialectics’ means simply ‘the art of dialogue’, i.e., knowing how to argue. Plato elevated this ‘technique’ to the noblest position in his scale of science, as something like ‘the understanding of the logical relations between some Forms and others’. But there seems to be a tension between what he reproaches to geometry so that it can not be the ‘purest’ science (i.e., that it proceeds step-by-step, in an argumentative fashion, taken for granted assumptions that later we shall see named as ‘postulates’, in Greek axiómata), and the fact that the purest science is for him the art of dialoguing, which also occurs essentially step-by-step (the prefix dia– has this precise meaning both in dialektikē and in diánoia). Perhaps he is mixing here the process of dialectics with its goal, which would be the intellection of the pure Forms, something like the aha! moment we might experience when we understand something… or rather, when we understand everything, for understanding something consists in understanding its relations to everything else, so it is not possible to have a ‘complete’ understanding of a ‘portion’ of reality.

In a nutshell, Plato’s view of ‘the sciences’, the first systematic theory we have about what they are and how they are attained, consists in proposing us a kind of scale of knowledge, from mere dreams to more or less solid opinions about material things, to cleverer mathematical constructions and demonstrations (all of which only merits for him the qualification of ‘arts’), and finally, to the only thing that would deserve to be called ‘science’: the deepest understanding of ‘the Totality’, which belongs into an ontological realm of eternal things, compared to which the material world in which we live is nothing but an absurd dream, a flawed image, a blurred shadow. Of course, you may be wondering what the two icons on the top of the figure (the Sun and the Good) may be standing for… but this will be the matter of our next section.

Thank Goodness!

**The Plimpton 322 tablet records Pythagorean triples from Babylonian times. / Courtesy Wikimedia Commons**

In the last section we introduced Plato’s model of the degrees of knowledge, ‘the simile of the line’, according to which the primordial difference between ‘science’ and ‘mere opinion’ is not so much about the ‘methods’ employed to reach one or the other (as will be assumed in modern times), but about the nature of the entities that are ‘known’ in each case: perishable, mutable, imperfect things that are perceived by our senses in the case of ‘opinion’ (dóxa), versus immutable, eternal, and perfect entities directly captured by our intellect in the case of science (epistēmē). We just cannot really know (in the deepest sense of ‘true knowing’) about material things or worldly events, because they are imperfect copies of the essentially and intrinsically ‘knowable’ objects of the true sciences, those that deal with entities that are immaterial and unchanging, entities that populate a separate realm, different from the empirically given natural world. This, as we saw, has an immediate disgraceful consequence: the fact that, according to the Platonic conception, there cannot exist something like a ‘natural science’ properly speaking, for, as we might say, “knowledge of imperfect things is always imperfect knowledge”.

We can conjecture that this unhappy result of Plato’s view of science had its roots in his identification of the notion of ‘science’ with the best developed science of his time (and, actually, the only really ‘developed’ one): mathematics, or geometry more exactly. The Pythagorean theorem, for example, is universally true (‘universally’ in the sense that it is true of all ‘true’ right triangles, and that its truth does not depend on circumstances like location or time… at least in the Euclidean space, we know), perfectly true (the equality it expresses is not ‘approximated’, but absolutely exact), as well as certainly true (there is no possible doubt about whether a right triangle obeys it or not). Its truth, furthermore, is not captured by the senses (we do not learn it by just observing many right triangles, nor by measuring and comparing their sides), but by our intellect or reason, hence it is an intellectual truth; remember that, according to the simile of the line, sense perception can only offer us pístis (“belief”), but not sure knowledge (epistēmē). Plato was convinced that scientific knowledge should always be at least of the kind we have about the Pythagorean theorem, and that everything falling short of that didn’t deserve to be considered ‘scientific enough’. And since some examples of that kind of knowledge were available in his times, why not assume that we had opened the road to the ‘noblest’ kind of knowledge, and that we might discard all that is of ‘inferior’ quality? Mathematical knowledge (and -do not forget it- that kind of science that for Plato was the supreme of all: the ‘dialectical art’ that allowed us to capture the logical relations between all possible ideas) can of course be ‘applied’ to material, concrete, mundane things, but in this case its outcome is always uncertain and debatable: perhaps we have not taken accurate enough measurements, perhaps we have not taken into account important facts, or perhaps someone has deceived us with the data. This is, hence, the reign of sophistry, that we saw exemplified in a previous section, not that of real science.

But let us return to the point that, in my view, is the most important to understand Plato’s cogitations: the fact that the difference between better or worse kinds of knowledge depends basically on the fact that some entities are more perfect than others. This brings us to the important aspect of the simile of the line we did not discuss in the previous entry: the role of ‘the sun’ and ‘the good’. According to Plato, the most characteristic property of the sensible things is… well… that they can be perceived by the senses, and most specifically, that they can be seen. And what is what allows us to see the visible things? Of course, it is light. And what is the ultimate and more powerful source of light? Obviously, it is the sun. Hence, the sun is in some (not totally metaphorical) sense what makes visible things visible, it is the ‘cause of visibility’. Understanding knowledge (even intellectual knowledge) on the model of perception (in the sense that, for Plato, all knowledge reduces to ‘grasp’ something), he assumes that something in the intellectual realm must be playing a role that is analogous to that the sun (or light) plays in the physical realm; i.e., there must be something that is what makes intellectually cognizable things ‘graspable’ by our minds (or ‘rational souls’), something that causes their ‘graspability’ or ‘intelligibility’. (By the way, if you are wondering what conclusion would Plato have reached if, instead of sight, he had taken another sense, like hearing, smell or touch, as its main model of sense perception, you are advancing a very pertinent conundrum, which I will not try to ask here).

Obviously, ‘the Good’ (or the ‘Form’, the ‘Idea’, or the ‘Aspect of the Good’), or more exactly, ‘Goodness itself’, is according to Plato what plays such a role. For, in the same way as visibility is the most characteristic feature of material things, perfection is the most essential aspect of intelligible things, as we have stated above. Hence, what allows our rational minds to understand the intelligible (or ‘understandable’) is the combined fact that they are perfect and that our minds capture the essence of perfection, the knowledge of what perfection is. Geometrical right angles are ‘perfect’, whereas the ones you more or less clumsily draw on paper are not perfect; and in recognizing this difference, you reveal that you have an implicit understanding of the Idea of Perfection itself. Actually, this was probably for Plato his most important ‘philosophical discovery’.

In another of his dialogues, Phaedrus, he depicts Socrates telling that in his youth he was a fan of Anaxagoras’ theory of nature, because he had heard that, contrarily to other ‘naturalist’ pre-Socratic philosophers (or ‘physiologues’, as Aristotle would name it a generation afterwards), the latter attributed the ultimate role in his explanation of Nature to what he called ‘the Noûs’ (Intellect). Unfortunately, once Socrates started examining the details of Anaxagoras’ theory, he found that all his explanations were in the end very ‘mechanical’, like those of most other pre-Socratic (and most explicitly, those of the atomists, like Democritus, that Plato does not even deign to mention), for all natural processes were rationalized by Anaxagoras as mixtures of different natural substances (of which, contrarily to the atomists, or to those defending the theory of ‘four elements’, like Empedocles, he, Anaxagoras, thought were almost infinite in variety); even noûs was conceived in that theory as a kind of fluid impregnating everything! So, nothing really intelligible had any working role in those explanations… what allows us to see that, for Plato, and probably for Socrates before him, ‘intelligibility’ had to be essentially connected to what we now call teleology: the world had to respond to a plan, a conscious, deliberate plan, in order to be truly intelligible. We can understand Plato’s philosophy of science, hence, as the attempt to fulfil that Socratic dissatisfaction, so that his ‘Idea of the Goodness’, as the intuition that the world must have a rational explanation, in the sense that it must somehow be the outcome of a process of reasoning, became the very nucleus of his worldview. Needless to say that this ended having profound, and not always fortunate consequences in the development not only of western philosophy, but of science itself. (By the way, if you are wondering why Plato was driven mad by a physical theory -i.e., a theory about nature, or physis– lacking an explicit role for ‘deliberate goals’, but was very delighted instead with a mathematical theory that was happily unconcerned with any reference at all to something like goals, plans or ends –téloi– in the proofs of its theorems, you are again advancing a very pertinent conundrum, whose answer might have something to do with what I will tell in the next section).

What a Beautiful World!

**Athanasius Kircher’s map of Atlantis from *Mundus Subterraneus* (“The Subterranean World”) (1669), drawn with south at the top. / Courtesy Wikimedia Commons**

We shall conclude with this section our discussion of Plato’s view of science, the main conclusions of the two former ones being, in the first place, the idea that ‘scientific knowledge’ (epistēmē) consists in the knowledge of eternal, intelligible Forms, whereas material things are imperfect copies of the former, and only graspable with an imperfect species of knowledge (‘opinion’, or dóxa), and, in the second place, that the ultimate foundation of scientific knowledge is the understanding of perfection itself, and, most specifically (applied to the knowledge of the material world), the understanding of how things, and the world, are teleologically organized. Of the immense literary production of Plato, there is only one of his ‘dialogues’, apparently one of his last works (the Timaeus), where he offers a more or less detailed exposition of his views about ‘natural science’, and it is there where we must turn now our attention.

Of course, it is impossible to give in this short entry an insightful summary of all the richness (and intricacy, often bordering incomprehensibility) the Timaeus contains, including the famous legend of Atlantis and all the details about the creation of the body and soul of the World, the creation of gods and men, etc. I shall only concentrate in the aspects of Timaeus’ exposition that have the closest connection with the topic of our series, i.e., those that make clearer Plato’s philosophy of science. As it is well known, Plato introduces in this work a kind of mythological figure (the ‘Demiurge’, meaning ‘artisan’) as the responsible for the creation of the cosmos. The mythical character of Plato’s narrative does not allow to determine with certainty to what extent his description of the cosmogenetic process has to be understood more or less literally, or more or less figuratively, as only a kind of ‘allegory’ in the spirit of the ‘simile of the line’ we saw in the past couple of entries, or the classic ‘myth of the Cave’ also in The Republic. Be it as it may, the very fact that Plato feels compelled to frame his explanation into a mythological story gives us a clear hint of what he thought ‘natural science’ or ‘physics’ must (or can) consist in: nothing close to the ideal of exactitude and demonstrative rigour that mathematics had in his own times, or physics itself attained one century later with Archimedes (not to speak of Galilei or Newton), but only something that corresponds, at most, with a merely ‘literary’ standard of argumentation. After all, for Plato knowledge of the material world is intrinsically ‘imperfect’ knowledge, as we have repeatedly seen, and he seems not to have imagined the possibility of a ‘natural science’ more rigorous and accurate than that.

It is true that the Platonic Academy started the idea of astronomy as an attempt to ‘save the phenomena’, i.e., to explain the apparently irregular movements of the planets with the help of precise mathematical models, something that (as we shall see) led centuries later to the development of very precise theories and to the appreciation of exactitude, like in the case of Ptolemy, but Plato himself seems to have been satisfied with (and, more importantly, he seems to have considered that it was impossible to aspire to anything better than) a merely ‘qualitative’ and loose agreement between the mathematical constructions of cosmological theories and the astronomical observations (or ‘phenomena’). Hence, we have not to see in Plato’s view of natural science the notion that ‘accurate predictions’ (and still less ‘unexpected predictions’) is one of the goals of physics, nor even a reasonable goal.

However, Plato’s efforts to ‘rationally explain’ the natural world led to some astounding ideas that (two millennia in the future) greatly influenced the development of modern physics, and that can only be interpreted as a work of absolute genius. We can start by recalling the final reflection of our last entry: how is it that (as in the Phaedrus), Plato frequently grumps about the lack of ‘rationality’ (in the sense of intentional design, or teleology) in other philosophers’ accounts of nature, but instead finds totally alright the absence of such ‘intentionality’ in mathematics? (I mean, couldn’t the natural world be as ‘rational’ as the ‘mathematical world’, without nothing in it resembling an ‘intentional order’?). The answer to this puzzle Plato allows us to glimpse is that ‘the Good’, the supreme Form, is exactly the same as ‘the Beauty’: the Demiurge’s ‘goal’ in giving shape to the world is nothing other than the desire of creating the most possibly beautiful cosmos. All other ‘goals’ or ‘plans’ we can find out within the universe, from the teleological organization of living beings, to the organization of political activities, just to quote a couple of prominent examples, are what they are, according to Plato, as the result of the most basic ‘goal’: that the universe must be as beauty as it can be. Taking this into account, it is not very important whether the ‘creation myth’ narrated by Plato in the Timaeus is understood literally or not, for what is relevant is the idea that beauty is the supreme force in the organization of the cosmos, and perhaps all the story of one god creating the earth, the sky, the people, etc., as a potter creates a vessel or a krater, may have been composed to be taken as just a metaphor. Hence, in philosophy of science, Plato is not only the founder of the teleological paradigm of scientific explanation (one that isn’t living its best moments, to say it all), but also the father of the idea that beauty is the most important virtue a scientific theory must have … because the ultimate truth about the universe must be perfectly beautiful (another idea that, though not as popular now as it has been, hasn’t ceased to exert a powerful influence in fundamental physics).

**Medieval manuscript of Calcidius’s Latin *Timaeus* translation. / Courtesy Wikimedia Commons**

Timaeus offers many examples of how the search of the maximal beauty constrains the Demiurge’s efforts to shape a lovely world (from the parts of the human organism, to the sizes and organization of planetary orbits –which, obviously, include those of the moon and the sun in Plato’s geocentric system–), but probably the most exciting one is the argument that leads to Plato’s theory of matter: the Demiurge would have attempted to create solid bodies in the most simple and elegant way, which reduces to the construction of the two most simple right triangles from which the regular solids can emerge; these triangles are an isosceles whose acute angles are 45º (so that two of them joined by their hypotenuses form a square) and one whose smaller cathetus length is half of its hypotenuse (so that two of these triangles, joined by their bigger catheti, form an equilateral triangle). Leaving aside the question of why Plato didn’t see the equilateral triangle as ‘elementary enough’, so that it felt the need to ‘derivate’ it from a ‘simpler’ geometrical form (its half), it’s clear how these figures allow the construction of the four regular solids Plato considers in his cosmology: the tetrahedron (four equilateral triangles), the octahedron (eight), the icosahedron (twenty), and the cube (six squares). He had the inspiration of equating each one of these solids to one of the classical ‘elements’ first introduced by Empedocles, and persistent in almost all the scientific views of the world till modern times: in this order, fire, air, water and earth.

Most surprisingly, Plato doesn’t feel totally happy with a theory according to which matter is organized according to a precise mathematical rule (a thesis that, no need to remember, is absolutely essential to modern particle physics), but insists in the fact that material things are intrinsically and necessarily imperfect (i.e., imperfect copies of true mathematical objects), and provides an astonishingly profound conjecture about what the ultimate cause of this imperfection could be. According to him, the lines and surfaces defining the ‘elementary triangles’ cannot be perfect, eternally stable (we would say), because they are ‘made of’ an ‘imperfect’ substrate he often calls ‘the receptacle’ (hypodokhê), or, most simply, ‘space’ (khôra, which perhaps translates better as ‘empty space’), and to which he very often refers with some feminine attributes as ‘mother’ or ‘nurse’, as well as with the name ‘anánke’ (‘necessity’, probably in a sense closer to ‘need’ or ‘lack’, nothing to do with ‘determinism’). This ‘receptacle’ is far from being comparable to the Euclidean absolute, and absolutely inert space of Newtonian mechanics, but is, instead,

not only shaken by the things it contains [i.e., the atoms of the four elements], so that it lurches haphazardly all over the place, but its motion in turn further shakes them. This stirring causes them to be constantly moving in different directions and to become separated. It’s like when things are shaken and sifted by sieves or other devices for cleaning grain. (Timaeus, 53e).

Hence, space is for Plato a kind of eternally moving but chaotic force that permanently ‘shakes’ in fortuitous ways the objects ‘made of’ it, i. e., the lines, surfaces and solids constituting the material atoms. Is not that wonderfully similar to contemporary ideas about ‘quantum space’ or ‘space-time foam’? I only leave this comparison for your consideration.

The last and, from my point of view, more important aspect of Plato’s contribution to the development of the ‘idea of science’, is the fact that with his geometric account of the ‘four elements’, he provides the first great example of what much later will become one of the identity signs of modern natural science: the idea of progress by theoretical unification (or ‘consilience’). After all, what Plato is achieving is nothing less than assembling a wonderfully unified framework of three of the most important insights of the natural philosophers that came before him: Empedocles’ theory of the elements, Leucipus and Democritus’s theory of the atoms, and the Pythagorean conjecture that nature is made of numbers or mathematical entities. These three theories were before Plato totally unconnected to each other: for example, Democritus believed that atoms came in infinite different forms, their shapes having nothing ‘mathematically special’ at all. Instead, Plato provides a very simple explanation (implausible as it unavoidably sounds now to us) of why there are exactly those four elements, i.e., those four types of ‘atoms’ (though probably Plato would rather apply the term ‘atom’ to the edges of his polyhedra). We should wait till the time of an Isaac Newton to witness a comparable move in the history of science.

By the way, if you are wondering what Plato thought about the fifth regular polyhedron (the dodecahedron of twelve regular pentagons), the only, and mysterious thing he says about it is that

one other construction, a fifth, still remained, and this one the god used for the whole universe, decorating it with figures. (Timaeus 55c).

Plato’s Best Student

**“Aristoteles” (1811) by Francesco Hayez (1791–1882). / Courtesy Wikimedia Commons**

If Plato’s reflections on the nature of epistéme was the starting point of what we can take as an authentic ‘philosophy of science’, and even if his views were probably the most influential during the rest of the Ancient times (as we shall confirm in subsequent entries), the truth is that science as we know it, and the philosophical understanding thereof, had its first real hero in Plato’s most distinguished disciple: Aristotle (384-322 BC). Aristotle started to study within Plato’s Academy as little more than an adolescent, and remained there, turned into one of its most outstanding educators, till Plato’s death, when Aristotle was in his late thirties. Rumours tell that the former pupil departed due mostly to jealousy for not having been appointed as the successor of the master in the Academy (a position that was given to Plato’s own nephew, the philosopher Speusippus); be it as it may, Aristotle moved to several places in the east and north of the Aegean for the next fourteen years (including a period as tutor of the future Macedonian king, Alexander the Great), till he decided to return to Athens to establish his own philosophical school, the Lyceum, which he run for another twelve years. He abandoned the city after Alexander’s death, for fear of anti-Macedonian sentiments (Aristotle was not a Macedonian himself, but his friendship with the Macedonian royal family was probably a very dangerous liaison), and retired to his estates in the isle of Euboea, where he died within just one more year, probably from an abdominal cancer, at the age of sixty-two.

In a way, Aristotle’s ideas are difficult to disentangle from those of Plato. Reading in parallel the surviving writings of the two intellectual colossi (different in format and conception as they undoubtedly are), it wouldn’t be difficult to imagine that they represented the evolving work of one single author, elaborated in two different types of books: Plato’s dialogues are literary masterpieces, most of them targeted to what we could label a ‘normal reader’ (of whom not too many must have existed at the time, however), and, with few exceptions (like the Timaeus, the Parmenides, or the Sophist), do not contain bookworm paragraphs as those typical of ‘scientific treatises’, i.e., full of logical detail, complicated terminology and systematic reasoning. Aristotle’s preserved works are, instead, just that kind of ‘scholarly monographs’, which use to start by clearly stating one problem, by discussing later the theses of previous authors, presenting the relevant data, and finally offering an analysis and a solution based on a given set of systematic concepts. Nothing similar to this style of ‘academic writing’ is preserved from before Aristotle’s times (except a few Hippocratic medical texts, and perhaps some short mathematical treatises), and at least in this first sense (we shall discuss other, more important senses later) we can bestow Aristotle with the title of ‘the founder of science’. He was, at least, one of the first to think and write ‘as a scientist’. Aristotle wrote also dialogues ‘for the general public’, and it seems they were highly praised by their elevated prose, but unfortunately none of them survived the Antiquity.

Nonetheless, as I was saying, regarding the content of Aristotle’s works, it would not be too fanciful if someone reached the conclusion that they belonged to the same author (or at least, to the same ‘school’) as the Platonic dialogues, only that they are probably more ‘mature’: some ideas appearing in the dialogues, as, for example, the theory of Form, are explicitly criticized by Aristotle… but they are also criticized in other dialogues by Plato himself, like in the Parmenides (where, by the way, a character from Socrates times but with the name of ‘Aristotle’ also appears), and with arguments that Aristotle will almost literally repeat in his Metaphysics. These ideas are also formulated in Aristotle’s writings ‘for the experts’, rather than ‘for the public’, as we have seen. One has often the impression that what Aristotle is doing is something like saying: “well, the theories, ‘similes’ and ‘myths’ presented in the dialogues are certainly very naive, imprecise and ambiguous, and this is the way in which they should be rationally formulated in order to take into account all possible criticisms”. It is, in a way, as if the disciple was trying to ‘tiding up’ his master’s rather ‘poetic’ thoughts. (For a philosophical and philological authoritative argument about the intimate connection between Plato’s and Aristotle’s thought, especially in the case of metaphysics, see ¹).

In the case of our series’ topic, the nature of science, Aristotle replaces Plato’s ‘simile of the line’ with a version which is much less speculative and flamboyant, but that in a way preserves its essential aspects: he also says, like Plato, that there are different ‘degrees’ of knowledge that we can order from the most ignoble to the most excellent, and that form a kind of ‘scale’ we should ascend: in Aristotelian terms, these ‘levels’ would be perception, memory, experience, art (téchne) and science (epistéme). The most important difference between them is not so much the ‘type of reality’ they respectively capture (though in a sense something of this is preserved in Aristole’s theory, as we just will see in a moment), but the amount of reasoning capacity they confer to us: from perception and memory, that only allow some kind of reactive behaviour more or less complex, to téchne and epistéme, that allow us to explain what we are doing… the characteristic aspect of epistéme being its capacity of providing with demonstrably true answers to why-questions: having science consists, for Aristotle, in knowing why things are the way they are. This is possible thanks to our grasping of the essence of things, i.e., of their more intrinsic, universal and unchanging nature. The aim of science is, hence, knowing in detail the nature of things… what, by the way, offers the first important difference with respect to the theories of Plato, for, as we saw, this author, thinking that the material world was only an imperfect copy of the world of eternal Forms, hesitated about the possibility of ‘a real science of nature’. Aristotle, instead, not only thought that a scientific study of nature was possible, but went so far as devoting most of his time to create just that… what we now call biology, and in this sense he certainly went much far beyond Plato. But this will be the subject of a future entry.

The Invention of Biology

**Landsat image of Lesbos. / Courtesy NASA, Public Domain**

During the time Aristotle spent far from Athens after the death of Plato, he lived for a few years on the island of Lesbos and in some Asia Minor cities that surrounded it, an area where a kind of ‘franchise’ of the Academy had been founded a few years ago under the patronage of the tyrant Hermias of Atarneus, who became one of the dearest friends of Aristotle (until his torture and crucifixion by the Persian king in 341 BC), and with whose niece Pythias the philosopher became lovingly married. Pythias, as well as one young student from Lesbos, named Tyrtamus (and that Aristotle renamed as ‘Theophrastus’: ‘of Divine Speech’), became his closest collaborators in the next years, though Pythias died relatively soon, nearly after Aristotle’s return to Athens in 335, whereas Theophrastus survived him for almost 35 years as his successor in charge of the Lyceum.

Aristotle’s interest in the living beings had surely started during his stay in Plato’s Academy, but it was probably in Lesbos when, far from the contact with other scholars more immersed in abstract and metaphysical discussions, he concentrated most of his intellectual activity into the direct study of animals, starting the immense work that now occupies more than one half of all of his preserved writings. Lesbos, in particular, has a couple of almost closed big lagoons (or albuferas) ¹ , the gulf of Kallonis and the gulf of Teras, where life thrives, and where fishers could be constantly providing him with both specimens and experiences (empeiríai, what –we must recall– he placed just in the middle of his ladder of knowledge, between the extremes of ‘perception’ and ‘science’). Scientific knowledge, for Aristotle, comprised two essential elements: knowing-what, and knowing-why. Of course, the second was for him the most excellent, but, he thought, it was worthless to speculate on the ‘whys’ without the most possibly detailed knowledge of the ‘whats’, and life offered, once a philosopher started to go to the trouble of looking deeply into it, an infinite variety of wonders to discover. Aristotle might have considered that, if we want to understand the world (which was the main goal of philosophy), we must particularly fix our attention in the most wonderful and complex part of nature, the living beings, rather than in more abstract and ‘simple’ entities (like those of mathematics and astronomy, not to speak of ‘the elements’), that had fascinated Plato and most other philosophers before him.

Hence, Aristotle started to elaborate a kind of work that his teacher would surely had considered boring and uninstructive, not to say vulgar: a meticulous catalogue of the peculiarities of animals, their parts and their kinds, the working of their organs and of their reproduction, their habits, their differences, and their similarities. Not all of this work has survived (for example, an impressive collection of anatomic charts and diagrams, accompanying the written text of other treatises, and very likely produced with the help of his wife, Pythias, was probably lost before the end of the Ancient times), but his books, known to the Christian civilisation by their Latin titles Historia animalium, De partibus animalium, De motu animalium, De generatione animalium, etc., became the main source of zoological knowledge for the following two millennia, and were praised as profound masterpieces even by Darwin himself. Of course, this knowledge-of-the-what-kind about animals can only be obtained by very different methods that knowledge about triangles, stars, or ideas of justice: one can’t avoid but getting ‘dirty hands’, for not only ‘field observation’, but systematic dissection, and even vivisection, had to be carried out by Aristotle and his collaborators, in order to grasp what was there, and what happened, within those complex things animals are. In one vivid example, something we might consider as the first ‘controlled experiment’ in the history of science is reported by Aristotle: the vivisection of chicken eggs after one, two, three days… till their eclosion in the 21^st day, in order to observe and register the development of the embryo.

One fundamental thing Aristotle verified when studying the animals was that, in spite of being very different, their variety seems to be arranged in a kind of hierarchical organisation, one that allows to describe ‘genera’ of bigger or smaller ‘generality’, from the most encompassing ‘kingdoms’ (to use a much more modern term), to the most differentiated ‘species’ (a concept, instead, that he didn’t only employ –of course, in his Greek tongue: éidos–, but that had been used by Plato as one of the names he used to refer to his eternal ‘Forms’, or ‘essences’). And, more importantly, this classification was not merely ‘logical’, or ‘arbitrary’ (in the sense that we may order and classify a set of things according to whatever list of properties they have), but something inscribed into the very nature of the things, making some groupings ‘natural’, and other ‘artificial’. For example, both humans and ducks are ‘bipeds’, contrarily to foxes, but humans belong into a natural group with foxes (the group Aristotle called ‘viviparous tetrapods’), whereas ‘bipeds’ is a category lacking biological relevance as for the most natural classification of the animals. Hence, some features and similarities between different animals are more important than others, ‘biologically speaking’, because they are more directly related to the essence of each species; and so, an adequate science of the animals has to start not only by a ‘rational’ classification (some derived from a merely speculative play of ideas), but with a detailed observation and comparison of their characteristics that leads to a natural ordering. The science of nature begins, hence, by ‘carving nature at its joints’ (an expression that, in fact, comes from Plato’s Phaedrus).

By the way, Theophrastus, who focused his own scientific research on plants and minerals, confirmed later with some discomfort that a ‘natural classification’ was much harder to find outside of the animal kingdom, especially in the case of ‘rocks’. Both he and Aristotle didn’t suspect, obviously, of the essential role that genetic inheritance and evolutionary processes had in the creation and in the distinctness of biological kinds. Theophrastus was also a little bit sceptical (though not too much) on his teacher’s main idea about what is what grounds the ‘naturalness’ of natural classifications. Remember that, for Aristotle, scientific knowledge consisted basically in knowing-why, or knowing something’s causes. He is also famous for his theory of ‘the fourth (types) of causes’, i.e., four ‘avenues of explanation’ we might give of a fact: the material (what is something ‘made of’), the formal (what its ‘structure’ is), the agential (who ‘did’ it), and the final cause (what is the purpose of the process), but, following the vision of Plato, Aristotle gave supreme importance to the latter type of explanation: “nature does nothing in vain”, he wrote repeatedly; all aspects of the world, and in particular, all the features of animals, should be ultimately explained by their function. Of course, living beings are (outside artifacts) the paradigmatic type of entities where parts are best understood by their contribution to the ‘working’ of the whole, and hence, where teleological explanation is most useful; actually, the word ‘organon’ (in Greek, ‘instrument’) was given by Aristotle its technical, biological meaning of ‘body part’ that now is prevalent. Instead, the old Theophrastus ended recognising that some features of living beings have probably no function at all (for example, males nipples), and much more examples outside biology (tides, to mention just one), and hence other forms of explanation should be pursued in these cases.

I shall lastly mention that, even if ‘biology’ is his dearest intellectual child, Aristotle, as his master Plato before him, thought the duty of a philosopher was to offer a scientific ‘theory of everything’, and hence his vision of natural science was essentially connected to a global understanding of the world and of science in general, and it is this connection what we shall examine in the following entry.

In Search of the First Principles

Besides being one of the main pioneers of scientific thought, Aristotle is the author of the work that can unquestionably be considered the first book explicitly and exclusively devoted to what we can call ‘philosophy of science’. This small book is known by the rather insipid name of Posterior Analytics (Ἀναλυτικὰ ὑστέρων), though, as in many other cases of Aristotle’s works, it is not clear whether that was the name he gave to the work himself (what is not utterly unlikely), or just the way it was denominated by his works’ Ancient editors. ‘Posterior’ refers, of course, to the existence of a different work called Prior Analytics (Ἀναλυτικῶν προτέρων), in which he created none other than a whole intellectual discipline, that of Logic. Together with a few other treatises, the Analytics constituted what later scholars, most essentially in the Middle Ages, knew as the Organon (or “instrument”), and which established for nearly a millennium the ‘rational way of thinking’. In a nutshell, the Organon includes an enquiry about the ‘elements’ of thought: concepts (in the Categories), propositions (in De interpretatione), and arguments (all the other books: besides the Analytics, or the exploration about the ‘demonstrative’ arguments, this includes Aristotle’s discussion of ‘non-demonstrative’, or ‘merely probable’ arguments in the Topics, as well as the ‘fallacious’ arguments in the Sophistic Refutations, these two books together can be considered as Aristotle’s theory ‘dialectics’, or ‘art of discussion’, to which we might join another work not traditionally included within the ‘logical’ books, the Rhetoric, about the use of arguments in order of persuasion in ‘practical’ contexts like trials or assemblies).

As I have mentioned in passing in the previous sections, Aristotle’s conception of ‘science’ is demonstrative knowledge of the causes that make it necessary that some general kind of fact is the way it is. The four concepts in italics are the fundamental ones. Starting by the end, science is always for Aristotle (as it was for Plato) some kind of universal knowledge, not knowledge about ‘the particulars’ (or the ‘instances’): we want to know why some type of things or events always happen in such and such way. We also attain ‘science’ when we show that this does not simply happens ‘always-but-by-chance’, say, but why it happens necessarily so. Hence, there is no role in this conception of science for something like ‘statistics’ or ‘probability’. We also may add that it would incompatible with this view doing something like a ‘historical’ science (or, to employ a 19^th century word, ‘idiographic’, from ἴδιος: “particular”, the same root as in ‘idiot’ or ‘idiom’), except, perhaps, by using properly scientific, i.e., universal knowledge, as an explanation of some singular events, or by employing this as an example of the former general principles. The concept of necessity is linked to that of causal knowledge: knowing why something happens as it does, is what gives us also the knowledge of why it couldn’t have happened otherwise. I will come back to the notion of cause at the end of the entry, and will comment now the remaining essential element of the Aristotelian view of science, that of demonstration, which is probably what most clearly allows distinguishing scientific from other kinds of knowledge (like perception, experience, or ‘art’, i.e., téchne).

This idea of demonstration is what links the prior and the posterior Analytics, for the idea is that scientific knowledge of a determinate proposition is our having a logical proof of it, or, to say it in mathematical terms, proving that it is a theorem. The Prior Analytics establish how this can be done in principle, for what that book performs is a systematization of all the possible ‘demonstrative arguments’ (what Aristotle calls syllogisms)… under the assumption that all the propositions we are considering have one of the following four structures: “every S is P”, “no S is P”, “some S are P” and “some S are not P” (“S” stands for “subject”, and “P” for “predicate”). For example, “every fish is an animal; every shark is a fish; hence, every shark is an animal”, etc. We do not need to enter into the details of Aristotle’s systematization of the valid syllogisms (besides admiring the immense genius he displayed in even considering the idea of such a system); suffice it to say that the notion of an item of knowledge being ‘scientific’ to the extent that it can be proved as the necessary conclusion of a valid chain of syllogisms elicits immediately a question to which Aristotle actually devoted an enormous chunk of his papiri: where do the premises of these argument come from? Demonstration is possible only if it starts from propositions whose truth is at least as certain and firm (or, as Aristotle says, more certain and firm) as that of what we want to prove thanks to them, but these first principles are, by necessity, indemonstrable in themselves (i.e., they cannot be ‘theorems’), and hence, our knowledge of them cannot be ‘scientific’ in the very same sense of ‘demonstrable’. Aristotle concluded that there must be some kind of knowledge somehow ‘superior’ to science (or epistéme), and it identifies it under the label of ‘intellection’ (noûs), though he seems to be content with offering just a kind of ‘psychological’ (rather than ‘logical’, ‘methodological’ or ‘epistemological’) account of it, by saying (in different parts of his works) that it is the final stage of different kind of argumentative processes, from ‘rhetorical’ or ‘dialectical’ ones (like when he ‘explicates’, in the Metaphysics, what is for him the first one amongst the first principles: the ‘principle of non contradiction’), or, in the case of ‘baser’ scientific principles (those of the ‘special’ sciences like biology, astronomy, etc.), as the result of what he rather vaguely calls epagōgē (‘induction’), not a really technical term for him, but just a way of referring to every kind of ‘argument’ that leads to a indubitable universal conclusion from singular examples or from other non-logically-demonstrative ways.

Though tons of ink have been spoiled in trying to elucidate what was exactly Aristotle’s ‘theory’ about the noûs, or the intellection of first principles, probably the closer to the truth is that he just failed to have a ‘theory’ about it, and assumed the existence of that type of knowledge as (to say it with a Kantian idiom) a ‘condition of possibility’ of (his theory of) science, i.e., something his own theory required, but were incapable of further justifying (a justification, by the way, that Aristotle probably considered as impossible as unnecessary, as the ‘scientific demonstration’ itself of the ‘first principles’). What remained, however, was this idea that the main goal of philosophy (as that intellectual activity whose most eminent product is science) should be the elucidation of the ‘first principles’. Actually, when philosophy and science started to be regarded as two different kinds of activity (instead of the former being just the pursuit of the latter), one way of putting out the difference between both was that philosophy should provide the axioms or principles from which science starts. But this is still many centuries ahead.

I will end, as I promised, offering a brief comment about Aristotle’s notion of cause. As it is well known, he says there are four types of causes: agential, formal, final, and material. Aristotle devotes some of the last chapters of the Posterior Analytics to explain and exemplify these four types of causal explanation. And, to our astonishment, the example he offers of ‘material cause’ is the explanation of the fact that… the angle inscribed in a semicircle is right! (the so-called Thales second theorem). But, what has this to do with ‘matter’? The solution to this paradox comes if we notice that, in that chapter (B.11), Aristotle does not use the expression ‘material cause’ or anything like that (what he does, instead, in most of his other works), but the rather cumbersome formula ‘if certain things are, then it is necessary that this thing is’. I would like to venture that this is the first historical appearance of a concept that was not fully developed till the 20^th century: supervenience. Hence, probably what Aristotle had in mind when talking about ‘material causes’ was something close to what we called today ‘supervenient properties’.

Epicurus’ Vessel and the Origins of Empiricism

**Dionysus on a ship sailing between dolphins. / Photo by Zde, Staatliche Antikensammlungen München, Wikimedia Commons**

One fascinating, as well as disconcerting fact about the evolution of Greek thought about science is that, almost immediately after the end of the ‘Classical’ period of philosophy, and particularly after Aristotle’s founding work on both philosophy and science, these two activities seemed to follow two radically separate courses. Actually, Greek science achieved its peak of creativity right in the so called ‘Hellenistic’ period, the epoch in which Greek culture became dominant in all the Eastern Mediterranean after the conquests of Alexander the Great, and concentrating a large chunk of its scientific production in the circle created around the newfound city of Alexandria, in the delta of the Nile (and, most famously, in his legendary Library, more aptly described as an advanced and global research centre). Of course, Hellenistic scientists worked also in other places (no other than Archimedes seems to have spent most of his mature life in his native Syracuse, a Greek city in Sicily, from where it regularly was in contact by ship post with his many colleagues in other cities), and, after the Roman conquest, many scientists and philosophers established themselves in the Caesars’ capital in search of wealthy patrons, though Alexandria persisted as the biggest hub of scientific investigation till the dawn of the Middle Ages. Athens, on the other hand, remained the chief centre of philosophical knowledge also to that time, through the centuries-old endurance of Plato’s Academy and Aristotle’s Lyceum, in combination and competition with other philosophical schools that also established themselves in the Greek metropolis only a few decades after Aristotle’s death, mainly the Epicureans and the Stoics (as well as the Cynics and the Skeptics, though these didn’t seem to have founded anything like a stable ‘institution’, like the others did).

It is not that the philosophers of the Hellenistic period didn’t care about the pursuit of scientific knowledge in fields like mathematics, astronomy, medicine, or the natural world in general (as we will see, that kind of knowledge was in some way very important for them), at least as compared to the importance they attach to moral philosophy. Probably, it’s rather that what we know as ‘science’ had started to become too complex, and to require a big measure of specialisation in order to master it as a competent researcher. In fact, all Hellenistic schools of philosophy emphasized the importance of ‘scientific’ knowledge for a variety of reasons, mainly the following two: in the first place, most of them attempted to offer a guide to the ‘good life’ in which something like ‘following nature’ was one of the fundamental ingredients, and hence knowing ‘how nature really is’ (or, say, ‘having and accurate cosmology’) became an important aspect of their teachings about how to reach such an ethical goal (though it seems that only the immediate successors of Aristotle, amongst the Hellenistic philosophers, devoted themselves to something like proper scientific research). In the second place, they also identified wisdom as the noblest ethical virtue, and the pursuit and enjoyment of knowledge became, in this way, an essential ingredient, if not the most essential one, in the picture of the character that archetypically embodied the best possible life: the ‘sage’. Mainly because of this, how to attain ‘real’ knowledge, and how to distinguish it from ‘mere opinions’, persisted as one of the main topics of philosophical discussion amongst the successors (and the rivals) of Plato and Aristotle, though, unfortunately, almost none of the written works of the philosophical giants of the 3^rd and 2^nd centuries BC (amongst many others: Epicurus, Pyrrho, or Zeno of Citium –the latter being the founders of the Skeptic and Stoic schools, respectively–), many of them monstrously prolific, has arrived till our times, and we have to painfully reconstruct their thoughts on this as well as on most other topics through the more or less reliable quotations, discussions and portraits made by authors writing several centuries afterwards, whose works, fortunately, have indeed survived.

For example, we know that Epicurus (341-270 BC) wrote a book (now lost) called The Canon, in which he explained his vision of how scientific knowledge has to be attained (and not only rationally exhibited or ‘demonstrated’, as Aristotle had done). His philosophy was deeply an empiricist, materialist, and (perhaps most importantly) anti-intellectualist one, denying not only the existence of immaterial souls or metaphysical realms in the style of Plato, but also that of ‘abstract’ entities and powers like Aristotelian ‘essences’ or the ‘nous’ (not in vein Epicurus’ doctrines were even described as ‘the philosophy of the populace’), but, nevertheless, it was based on a view of the world that was deeply unintuitive and shocking for the minds of Ancient people: a universe consisting in a infinite number of indestructible tiny atoms eternally moving at random in an infinite (otherwise) vacuum space. Hence, Epicurus needed a way to convince his readers and students that this shocking cosmology (with all the details about the working of the natural phenomena and human biology that were relevant in the Epicurean moral teachings, and for which we don’t have space here) is the inevitable outcome of a sound argument that has to start from facts everybody accepts. Because of the lost of his works, we ignore most of what Epicurus’ canonics (his name for ‘methodology’) might contain, but a few renditions of its two basic methodological rules are preserved (for example, in the relatively extended account of Epicurus’ life and doctrines in the 3^rd century AD famous biographer Diogenes Laertius’s –an Epicurean himself– book Lives of the Eminent Philosophers). These rules state more or less the following:

In order for investigation to start, we have to assume the ordinary meaning of the expressions we employ to describe the facts.
Investigation must proceed from what is observed, and infer about what is not observed (either because it happens in the future, or because it is intrinsically unobservable), according to the coherence or incoherence of these inferences with what we can observe.

**Photo of Otto Neurath published in 1919. / Courtesy The National Library of Israel, Wikimedia Commons**

To these rules we can also add a famous Epicurean maxim stating that “all sensations are true”. These three rules together allow us to glimpse a radically empiricist, coherentist and anti-foundationalist view of scientific knowledge. If we left Aristotle in the preceding entry wandering in search of ‘the first principles’ from which to start a true ‘scientific demonstration’, if we saw Plato despising the value of sensory perception in comparison of the splendour of reason, Epicurus invites to take at face value our ordinary experience and the meanings of the common words we employ to describe it. Reason may help to go further from ‘common sense’, and of course to revise it if some of its ideas go in contradiction with observations. In this sense, Epicurus’s view of scientific research is somewhat similar to one of the most well known images in the history of philosophy of science: Otto Neurath’s boat, that of our knowledge consisting in a floating framework of interconnected ideas that have to be constantly renewed on the go, without having the possibility of firmly grounding any of them on a solid basis. The tension in Epicurus’ theory between the ‘essentially-infallible sensations’ (aisthéseis) and the ‘just-by-default-acceptable ordinary meanings’ (or prolépsis) also recall a little bit of Neurath’s and other logical positivists debates about the nature of the ‘protocol sentences’ (Neurath’s position being that these are revisable, whereas others like Schlick and the young Carnap more sympathetic to the thesis that basic statements have to be void of any kind of ‘theoretical content’ and, thanks to that, firmly indubitable). Lastly, the role of observation as the only way to test whether a theory is acceptable or not (rejecting it if it contradicts the empirical facts), and the importance attached to the inference to what has not yet been observed (a kind of inference Epicureans call epilogismós, what we might translate, preserving the play of words with Aristotle’s concept, something like ‘ampliative syllogism’), is obviously a little bit resembling to Popper’s falsificationism, or even to the idea of ‘inference to the best explanation’ (or ‘abduction’), though I admit that all these comparisons require perhaps too much benevolence.

I finish by mentioning that a more extensive account of this ‘liberal’ view of ampliative, or abductive reasoning (or, if you prefer, ‘inductive inference by attending to similarities, to the testimony of many people, and to coherence with other inferences’) has been almost miraculously preserved in a roll (presumably entitled On phenomena and signs) that, together with many other ones, was carbonised in Herculanum by the 79 AD eruption of Vesubius, in the famous Villa of the Papyri. Many of these books contained the works of a ‘lesser’ Epicurean philosopher, Philodemus of Gadara, that publicised Epicureanism amongst the Roman elites during the times of Julius Caesar, and who probably was also influential in the adoption of this philosophy by the author of the other main source we have about the theories of Epicurus: Lucretius’ masterpiece of Roman literature, De rerum natura, whose Indiana-Jonesque rediscovery by the Florentine humanist of the early 15^th century Poggio Bracciolini has been excitingly narrated in Stephen Greenblatt’s book The Swerve, also a nice exposition of Epicurus’ doctrine and influence.

From Logical Stoicism to Logical Positivism

**Chrysippos of Soli, second founder of Stoicism. Marble, Roman copy after a lost Hellenistic original of the late 3rd century BC. / Photo by Marie-Lan Nguyen, British Museum, Wikimedia Commons**

According to the traditional myth, mentioned in passing in the first section of this series, contemporary philosophy of science would have started in the post-WWI Vienna, when a group of young philosophers and scientists, under the heading of Moritz Schlick, attempted to show how scientific knowledge could be unambiguously derived from observational data (or at least, clearly verified by these) with the help of strictly logical arguments. Also, according to this mythology (in this case, with more than a spoonful of truth), the plausibility of such an arrogant and overambitious project (that didn’t survive in those terms the disintegration of the ‘Vienna Circle’ Logical Positivism in the years previous to the Second World War) derived in good part from the apparent successes of another philosophical project started in the last decades of the 19^th century: Gottlob Frege’s so called ‘logicism’, or his attempt to ‘reduce’ all mathematics (or more exactly, set and number theory, and what can be derived from that) to ‘logic’ (for Frege, contrary to e.g., David Hilbert, didn’t believe that geometry could be so reduced). This project has had as younger champions figures of the stature of Bertrand Russell and Ludwig Wittgenstein, forming together with Frege and with physicists Ernst Mach and Ludwig Boltzmann the Vienna Circle’s book of saints (for a lively history of the Vienna Circle, see Sigmund, 2017).¹

As the story goes, this reductionist project was ultimately grounded on one of the most remarkable achievements in a century as formidable in intellectual feats as the 19th: the invention of ‘modern logic’ by Gottlob Frege (1848-1925) himself. What Frege did, in his juvenile book Begriffsschrift (or ‘Conceptography’, 1879), was to invent a new type of ‘logic’, a rather different one from the classical ‘syllogistic’ (or ‘term’) logic of Aristotle, that have been the canon of rational thinking for more than two millennia, and that now sounds better fitting into books of theology, metaphysics or law than into contemporary scientific works. Fregean logic, instead, consisted of propositions connected by ‘truth-functional operators’, like negation, disjunction, conjunction, conditional and bi-conditional, and where the propositions themselves are analysed in a structure that links ‘variables’ and ‘constants’ (i.e., terms for individual entities) by means of ‘predicates’ (i.e., monadic, dyadic, or polyadic relations) and ‘quantifiers’ (expressions like ‘for every x…’ or ‘for at least one x…”). If you have read almost any mathematical handbook written in the last century, you will be perfectly familiar with that type of logic, with sentences of the form ‘a relation R is transitive if and only if for every x, y, z, if xRy and yRz, then xRz’, or, in the standard symbols: ‘R is transitive ↔ (∀x∀y∀z (Rxy ⋀ Ryz) → Rxz))’ (by the way, Frege’s Begriffsschrift originally employed a much more clumsy typography, but the essence is the same).

Frege’s logicism failed as a project in the foundations of mathematics because of eventual results like Russell’s paradox (‘the set containing those and only those sets not belonging to themselves, belongs to itself or not?’) and mainly by Gödel’s incompleteness theorem (‘for every consistent axiomatic system formalising arithmetic there is at least a true arithmetic proposition that can not be derived from those axioms’). But this does not preclude that almost all contemporary logical research, as well as mathematics and computer programming, and everything that depends on them… which now is nearly everything in all scientific fields, remains now absolutely dependent on the new type of logic the Gottlob Frege devised in his Jena solitude (for his work was not properly recognised till many decades after its publication).

Fregean logic’s departure from the classical, Aristotelian one (Kant, one century before Frege, famously said that logic ‘had born complete out of the mind of Aristotle’) is so huge that it can be taken as the clearest example of a Kuhnian ‘paradigm shift’, one of the greatest innovations in the history of human thought… save because it (as almost everything) did have precedents and precursors. Historians of logic, once they became familiar with Frege’s contrivance, indicated soon a kind of family resemblance with the ideas of a fistful of (who else?) obscure Greeks, who apparently had developed something like a theory of arguments (or ‘dialectical art’) one century more or less after the great Aristotle. The main figure within this group was Chryssipus of Soli (c. 279-206 BC), the third leader of the Stoic school, that we had mentioned in the past section. His fame as a ‘logician’ (or master in the art of debating and arguing) was such in Ancient times, that the historian Diogenes Laërtius said that “if the gods used dialectics, they would employ that of Chryssipus’. Stoic logicians (and their own precursors, known as the ‘Megarians’, i.e., the disciples of Euclid of Megara –not to be confused with the mathematician Euclid of Alexandria, the former being a disciple of Socrates, and hence a contemporary of Plato) had defended a kind of analysis of arguments rather different from Aristotle’s syllogistics, and closer to what we (after Frege) call ‘propositional logic’, like for example modus ponens (if A entails B, and A, then B), modus tollens (if A entails B, and not B, then not A), or the ‘disjunctive syllogism’ (if either A or B, but not A, then B). Glimpses of this propositional logic (that Chryssipus had ‘reduced’ –i.e., axiomatised!– to just five formal types of propositional inferences from which all the other valid ones could be derived) had persisted through the centuries and reappeared in the writings of some medieval scholars, both Arabic, like Avicenna, and Christian, like Peter Abelard, and hence the idea of ‘a propositional logic’ was not something so absolutely new even in Frege’s times. The history of logic had also been a topic systematically studied (like almost everything imaginable) by the indefatigable 19^th-century scholars, in this case by one Carl von Prantl and his 4-volume Geschichte der Logik in Abendland (History of Western Logic, 1855-1870), a book the young Frege knew well.

**Karl von Prantl / Courtesy Wikimedia Commons**

Prantl’s Gechichte contains an almost one-hundred page section on the Stoic logic, collecting all the by-then known testimonies about those authors found in others’ works (for none of their original books –only Chryssipus is quoted has having authored around 700 works, 300 of them about logic– survives), though this didn’t seem to have arisen Prantl’s sympathies, for he (a good Aristotelian) repeatedly said that the Stoic’s ideas were just blödsinnig (‘idiotic’) and läppish (‘ridiculuous’). Obviously, Frege didn’t think the same, and, as it has been convincingly proved by historian of logic Sussanne Bobzien in a very recent paper² that has provoked a lot of quarrels in academic circles, it is not only that Chryssipus’ ideas loosely ‘inspired’ Frege’s developments, but that our German hero almost literally copied in many dozens of places from the relic-like surviving lines about Chryssipus’s insights. Of course, this does not reach the complex formal apparatus developed by Frege, that is so central to modern logic, but runs through most of the ‘philosophical’ discussions Frege’s work contains about things like the ‘nature’ of propositions as ‘units of thought’ (for the Stoics: assertibles, or ‘complete contents’), the nature of negation and logical connectives, or even one the ‘most Fregean’ innovations: the analysis of universal statements not in the Aristotelian way (‘All men are mortal’) but in terms of universal quantifiers linking ‘incomplete –or sub-sentential– contents’ (i.e., ‘If something is a man, then it is mortal’). In a different context, the similarities are so patent (as is Frege’s omission of quoting his sources) that we wouldn’t doubt in affirming that “Frege plagiarized the Stoics”, as Bobzien’s paper title itself claims.

Without entering here in the debate whether this is a real case of ‘plagiarism’ or not, the truth is that ‘Logical Stoicism’ didn’t seem to have derived into something similar to a full-blown philosophy of science like that of ‘Logical Positivism’. It is not that Stoics had nothing to say about science (as I mentioned in the last entry of the series), but that they were not attempting to a kind of ‘formal reconstruction’ of scientific theories from scientific data (as Schlick or Carnap tried), nor, of course, a ‘reduction’ of mathematical theories to logical arguments (like Frege and Russell attempted). Or, if they said or wrote something along those lines, it has not reached us at all. What is undeniably true is that Stoicism became something like the ‘official philosophy’ amongst the upper classes of the Hellenistic times and the first centuries of Roman power, and hence it is very likely that many, if not most of the scientists working during that period would have considered themselves as something like ‘Stoics’ in their philosophical leanings. But, as I have said, nearly nothing about how those philosophical ideas on logic might have influenced their vision of science has survived.

On Ancient Science and Scientific Progress, or Artemidorus’ Dream

**Mummy of a Greek youth, aged 19-21, named Artemidorus. 100-120 AD. / Courtesy British Museum, Creative Commons**

Just to take stock of what we have encountered in the previous entries of this series, regarding the ideas of contemporary philosophy of science than can find some kind of ‘ancestor’ in the works of ancient ‘philosophers’, we can mention Plato’s and Aristotle’s discussion about what are the essential differences and relationships between ‘scientific’ and other ‘lesser’ types of knowledge (like ‘opinion’ or ‘experience’), the former’s insights about the virtues of ‘theoretical unification’, as well as the latter’s analysis of the idea of ‘demonstration’ and of the different types of ‘causal explanation’ (including a rudimentary view of the notion of ‘supervenience’), and, going beyond the work of these two philosophical giants, we have also seen how the fundamental roles of empirical observation and careful logical reasoning (more than metaphysical speculation) were also established as the cornerstones of scientific research by the philosophers of the Hellenistic times. We also mentioned in the first entry of the series that there are stark differences not only between ancient and contemporary science, but on the philosophical understanding of the nature and structure of science: first, the institutional ‘entrenchment’ of science was very precarious in Greek and Roman times, as compared to how they become after the Scientific Revolution of the Modern Age, and especially after the State started to be its main patron in the 19^th and 20^th centuries, and hence most of science’s social aspects were basically out of sight for ancient philosophers (though not completely, as we shall see in a moment); and second, contemporary epistemologists are more aware than their ancient predecessors of the provisionality and mere probability of scientific knowledge, perhaps due to our having experienced the dethronement of many theories that once were considered the epitome of certain knowledge (but, as I shall comment, this difference is perhaps restricted to the philosophical interpretation of ‘knowledge’, and not a faithful description of the ancient ‘natural philosophers’ real attitude towards their attainments).

In this entry I am going to depart a little bit from what ‘philosophers’ (I mean, philosophers in their task of lucubrating about the ‘epistemological or metaphysical foundations’ of science) said about the topic, and will focus instead on the (‘philosophical’) view of ‘science’ held by ‘practicing scientists’ and ‘intellectuals’ widely understood had in the Ancient times. The many inverted commas in the preceding sentence are due to the fact that, by then, most of what is mentioned there was just named philosophy/philosopher/philosophical, and we have to attend mostly to what the relevant people did, in order to classify them more as ‘a scientist’ (the closer expression in the times would be physikos -or physicus, in Latin- what after all was just an abbreviation of ‘natural philosopher’) or as ‘an intellectual’ (i.e., somebody writing about these topics without pretending being in the task of providing us with anything close to a ‘philosophical grounding’ of knowledge, nature, or whatever). In conversations on this topic, the authors of the era often referred to those involved in that kind of ‘grounding’ as ‘theologians’, though we don’t have to bring to our mind the image of a priesty professor trying to give a patina of rationality to the religion he or she happens to profess, but rather someone like Plato (with all his other-worldly metaphysics) or even Epicurus (who also talked about the gods, though as blissful, eternal and dainty collections of atoms navigating the infinite space without worrying at all about human miseries). This rather reflects the common view in the Hellenistic and Roman era (though based on Platonic and Aristotelian ideas) that ‘theology’ was the ‘science’ of the first principles, and that ‘proper science’ (i.e., natural philosophy and mathematics, what Aristotle had called ‘second philosophy’) only came afterwards.

Hence, the fact is that, in the six centuries since Aristotle’s death till the climax of the Roman Empire before the almost mortal crisis of the mid-3^rd century, it is when ancient science produced most of its greatest discoveries, and the people of the era were evidently conscious of the fact that ‘philosophy’ (‘theology’, ‘metaphysics’, or ‘first philosophy’) was clearly lagging behind ‘science’ in terms of its fertility. Philosophical schools still reigned supreme in the intellectual domain, and wealthy people still sent their sons (much less their daughters) to Athens in order to be educated by the stars of the Academy, the Lyceum, or the Stoa. But as for the question of which one of these ‘schools’ had the ‘Truth’, the common consensus was that something like a permanent stalemate had been achieved, and an eclectic mix and balance of thesis and arguments about metaphysical questions (like that exemplified by Cicero) had become the most ‘elegant’ position amongst the literate classes. Instead, the same Cicero, as well as nearly every other author of the time, like Pliny, Strabo or Seneca, just to name a few, explicitly admitted that ‘science’ (including mathematics and ‘natural philosophy’, as the knowledge of the causes and forms of natural phenomena, from astronomy to agriculture, from medicine to engineering) not only had progressed in the past, but was still progressing, even if some of their results were obviously ‘better’ than others. Seneca, for example, confided that ‘in the future’, empirical investigation would finally settle whether it is the sun what turns around the earth or vice versa, and even expected that, at some point, science would allow us to discover planets and star so faint that they are invisible to the naked eye. They also believed that this kind of progress was the most characteristic feature of ‘science’, and that this progress would spread towards all aspects of human life, making it better and more comfortable (cf. Carrier 2017).

Surely, being this common-sense notion of ‘scientific progress’ more a ‘popular idea’ than a ‘philosophical concept’, the Ancients basically lacked a doctored view of what this kind of progress might consist in, in the sense of a sophisticated discussion about what were the logical relations between ‘successive theories’ (they even lacked the idea of ‘scientific theories’ as entities susceptible of ‘logical analysis’, beyond the nuances of a Chryssipus we saw in the last entry), a clear conceptual framework to understand the relations between ‘pure’ and ‘applied science’, or even a notion similar to that of Imre Lakatos’ ‘research programmes’ or Thomas Kuhn’s ‘paradigms’. But they, and in particular the ‘natural scientists’ (or physikoi) themselves, ended having a rather clear idea of how scientific progress can be attained. Perhaps Galen (2^nd-3^rd centuries AD), surely the most eminent medical scientist of the age, is the one that most clearly exemplified this, and his many ‘errors’ (mostly due to the impossibility, with the technics of the date, of understanding or manipulating anything in a living body that is so small that cannot directly be seen, like cells or biomolecules, or even capillaries) must not eclipse his astounding number of correct insights both in anatomy and in therapy. But I want to close this entry mentioning one much more obscure of Galen’s contemporaries: Artemidorus of Daldis (or ‘of Ephesus’, his real birthplace, though there were so many famous people from Ephesus, that he chose to be known after his mother’s city name).

Artemidorus attempted to establish a new science that were rationally grounded on the methods that had been proved to be successful in many other fields, from medicine to geography, from astronomy to zoology: systematic collection of experiences, without being tutored by metaphysical speculations or apriorist prejudices, whereas organised according to the most logical and rational arguments. As the bravest geographers and natural historians did, he travelled almost all the known world (from Rome to Levant, from Greece to North Africa) in order to gain knowledge from the experience of ordinary people and what we would call ‘village healers’, interviewing probably thousands of individuals, what, together with the reading of everything that had been written on the topic (what, by the way, he didn’t find very trustworthy), provided him with an impressive ‘database’ on which trying to build a logical system. His aim was no other than providing future ‘professionals’ with a guide that help them to make the best diagnoses and forecasts, bettering so the life of people as medicine and engineering had done and were doing. He wrote the most systematic book on the topic to date and for many centuries, perhaps not matched till the work of a well known author around 1900, though this was based on rather different hypotheses, of course. Artemidorus, however, though relatively more popular in the following centuries than most of the other scientific authors that had preceded him, was chronologically at the verge of the times of ancient science, and so he didn’t find successors of his ambition, cleverness and scientific talent, and hence his work became little more than a dream.

Sorry, I have forgotten to mention the topic of Artemidorus’ research, but you can easily infer it from the title of his book: Oneirocritica.

Bibliography

Aristotle, Posterior Analytics, Oxford, Clarendon Press, 2002.
Artemidorus, Oneirocritica (on the interpretation of dreams), Oxford, Oxford University Press, 2012.
Asmis, Elizabeth, Epicurus’ Scientific Method, Cornell University Press, Ithaca, 1984.
Aubanque, Pierre, 1962, Le problème de l’être chez Aristote, PUF, Paris.
Ayer, Alfred (ed.), Logical Positivism, Simon and Schuster, London, 1959.
Brisson, Luc, and F. Walter Meyerstein, 1995, Inventing the universe: Plato’s Timaeus, the Big Bang, and the problem of scientific knowledge, New York, SUNY Press.
Carrier, Richard, The scientist in the early Roman empire, Durham (N. Ca.), Pitchstone, 2017.
Diogenes Laertius, Lives of the Eminent Philosophers, Oxford University Press, 2018.
Greenblatt, Stephen, The Swerve: How the World Became Modern, Norton, New York, 2011.
Gregory, Andrew, 2001, Plato’s philosophy of science, London, Bloomsbury.
Harari, Orna, Knowledge and demonstration: Aristotle’s Posterior Analytics, Dordrecht, Springer, 2004.
Hippocratic Writings, ed. by G. E. R. Lloyd, Penguin, 1978.
Karl Sigmund, 2017, Exact Thinking in Demented Times: The Vienna Circle and the Epic Quest for the Foundations of Science, Basic Books.
Leroi, Armand Marie. The Lagoon: How Aristotle Invented Science. London: Bloomsbury, 2014.
Pickering, Andrew. 1995. The Mangle of Practice: Time, Agency, and Science. Chicago, The University of Chicago Press.
Sussanne Bobzien, 2021, “Frege plagiarized the Stoics”, in Fiona Leigh (ed.), Themes in Plato, Aristotle, and Hellenistic Philosophy, University of Chicago Press. pp. 149-206.

Originally published by Mapping Ignorance, 05.17.2021, under the terms of a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International license.

Matthew McIntosh

Administrator

Author's website Author's posts

Related Stories

Foretold and Controlled: Divination, Surveillance, and Social Order in the Ancient World

Marked and Watched: Identification, Surveillance, and Bodily Control in the Medieval World

From Pavlov to Public Relations: The Long Arc of Behavioral Manipulation in the 20th Century