

Examining different historical calendars and the origin of the western calendar.

By Karl Hagen
Independent Educational Consultant
Principles of Historical Calendars
Overview
Most historical calendars have been abstractions of the major observable astronomical cycles, especially the sun and moon. Widely different cultures often wind up with similar looking calendars, and at first sight it might seem as if direct influence were involved. While such may have been the case in certain instances, the conclusion is not necessary. If we consider the problem from the point of view of a hypothetical calendar designer, the possible calendars we can design are heavily determined both by the nature of the observed cycles and by the needs of our society. So what possibilities does our calendar designer have?
A Count of Days

The period which has generally been taken as basic for all calendars is the day (one alteration of light and darkness). To be more precise, the day to which we refer here is the solar day i.e., the length of time it takes the sun to reach the same spot in the sky again. Astronomers have traditionally used the sun’s zenith, i.e. noon, as the reference point, because it can be most accurately measured, and because an entire night’s observations can be recorded as occurring on a single day. The astronomers’ practice differs from the current civil one (where the new day begins at midnight), as well as ancient civil practices, which began the next day either at sunrise or sunset. If you are willing to deal with large numbers, all you really need for a calendar is a linear count of days from some starting epoch. Exactly such a count is often used by astronomers, the so-called Julian day, introduced by Joseph Scaliger in 1583. Julian Day 0 is defined as noon on Monday, January 1, 4713 B.C.E. (in the Julian Calendar). This strict day count is handy for comparing different calendar systems and making astronomical calculations, but rather awkward in ordinary life. It doesn’t really help people know when to plant their crops or when to celebrate recurrent festivals. The only society to use something comparable to the Julian date in regular practice were the Classic Maya, but even they supplemented their so-called Long Count with other cycles of a more manageable variety.
An Arbitrary Cycle

The next simplest possibility for a calendar (although not necessarily for the people using it) is a cycle of days of arbitrary length. The calendar can proceed by simply counting days, over and over, ad infinitum. We have just such an arbitrary cycle in our week. Notice that the cycle of week days runs independently of our other cycles of month and year. Another example is the nundinae, an 8-day interval used in the Roman republic. An arbitrary cycle need not be quite so simple (the Maya have a 260-day count), but its advantage is that we need not bother adjusting our calendar to keep it in step with the irregular periods of the sun and the moon.
A Solar Cycle

If you are a farmer, an arbitrary period has its problems. Of particular interest is the best time to plant crops—an activity tied to the seasons, which are in turn linked to the earth’s revolution around the sun. If all you have is an arbitrary cycle, it’s much more difficult to tell just when you should plant. Some agricultural societies, therefore, have tried to link their calendar to the length of the time it takes the earth to rotate around the sun. Of course most agricultural societies have not known that the earth orbits around the sun. From the perspective of an earth-bound observer, this motion (along with the tilt of the earth’s axis relative to its orbit around the sun) translates to the changes in position relative to the horizon where the sun rises (or sets) each day. Over the course of a year, this position will change, day by day. If you look East at sunrise, the point at which the sun appears to rise each day will move over a year between a maximum north and south position (the solstices). The midpoint of this motion, through which it passes twice each year, is the equinox. If you live within the tropics, at some point in the year the sun will pass directly overhead (i.e., at noon a straight stick will cast no shadow). The length of one complete cycle is known as the mean tropical year. In 1900 CE this period was 365.24219878 days, and the length of the tropical year has been shown to decrease by 0.0053 seconds per year (a value which becomes important when we start talking about 1000-year intervals).
So precise a measurement of the year, of course, would have been irrelevant to an early farmer, even if the astronomers could have measured it. A shift of five or ten days won’t really matter too much, since annual variations in the weather will be greater than that. Once the calendar is out by a month or more, however, problems will arise if the farmer depends upon the calendar. It doesn’t necessarily follow, however, that an agricultural society needs to keep its calendar tied, even loosely, to the seasons. Even if we assume that farmers really need someone to tell them when spring is coming, an alternate procedure would be for a specialist, for example a calendar priest, to announce when the proper planting time fell in the calendar.
A Stellar Cycle

An alternative to measuring the passage of the sun through a fixed point (equinox or solstice) would be to measure the appearance of a particularly prominent star or constellation, either just before sunrise or just after sunset. These events are called heliacal rising and setting and will yield a period that is fairly close to the mean tropical year. Such a measurement might seem like more work, but it can be handy, particularly if you live in someplace like the desert or a small island where the horizon is too flat to make a reliable measurement of the changes in the sun’s rising position. Old Hawaiian religious ceremonies, for example, began each year with the heliacal rising of the Pleiades. Over a long time, however, a calendar based on heliacal rise and set times will slip with respect to the solar equinox—this is the phenomenon known as the precession of the equinox and is the result of the top-like wobble of the Earth’s axis, which takes about 25,800 years to complete one full wobble. A year based on this kind of measurement is known as a sidereal year (sidus = Latin for “star”), and is about 51.15 seconds longer than the tropical year.
A Lunar Cycle

Just as a year can be defined relative to the stars or the sun, so can a moon’s orbital period. The length of time it takes the moon to complete one orbit around the Earth is 27.32166 days. From an Earth-bound observer’s point of view, this is the time it takes the moon to return to the same place relative to the stars, and is called the sidereal month. But because earth and moon are both moving around the sun, it takes the moon a bit longer to get back to the same position relative to the sun, and hence show the same phase (i.e., the amount of the moon’s disk illuminated by the sun). This period, the synodic month, is 29.53058773 days.
Lunar cycles were the most common basis for early calendars. These calendars were often not based on any mathematical determination of the synodic month at all, but relied, particularly in their earliest formulations, upon direct observation to determine the new month. So when do you define the month as beginning? The two obvious starting points are the new or the full moon. Since the astronomical new moon occurs appears so close to the sun as to be invisible, this gives us three observational possibilities: the full moon, the first crescent of the ascending moon after the new moon, visible at sunset, or the last crescent of the descending moon, visible just before sunrise. There is a correlation between when the next day is considered to begin and which observational choice is made. For a society that begins the new day at dawn, the first day the waning moon is invisible just before sunrise is a good time to start the new month. If the next day begins at sunset, e.g., the Jewish Sabbath, the first observation of the new moon makes more sense. A full moon observation would seem to imply a midnight start. Such observations can be used in either a lunar or a lunisolar calendar. It will result in months that generally alternate between 29 and 30 days, but because the synodic month is not exactly 29.5 days, the alternation will not be completely regular.
Direct observation does have its drawbacks. Clouds might obscure observation, and in a large civilization, there is a problem with ensuring each location stays in sync with the rest. The historical development of lunar and lunisolar calendars is largely a matter of replacing direct observation by mathematical formulas and tables that allow the prediction of the month’s start without the need for observation.
Lunisolar calendars have the additional problem of keeping the lunar months roughly aligned with the solar year. They generally do this by the insertion of a 13th, intercalary month at periodic intervals. Once again, in a calendar’s earliest stages, this intercalation was generally accomplished through decree from a central source. In later times, regular rules were developed.
Other Cycles
In principle, any astronomical cycle, e.g., the orbit of Venus or Mars, could be used to construct a calendar. In practice, very few societies bothered. These events were carefully recorded by astronomers, but only where these planets played an important role in religious observances (once again, see the Maya) were these events incorporated into the regular calendar.
Putting It Together
Imagine yourself as an early astronomer. Your local ruler has been funding your research for several years, and now he wants some practical results. Your job: make a calendar. Which cycles are you going to include? What approximations are you going to make?
Obviously some of your decisions will be based on just how precise your measurements have been, but even more on the needs of your society (and your patron, who is footing the bill, after all). You will need to account for any preexisting traditions. If your people have been counting seven-day cycles for hundreds of years, resting on the seventh day, they will probably not accept a change to a ten-day cycle, which is what was attempted in revolutionary France. Religious aspects and cultural conservatism aside, neither inconsequential, this change would mean fewer days of rest for people. You also might want to consider your own needs. A complex calendar that is constantly changing with respect to the solar year, for instance, might seem like a bad choice. But if you can get this calendar accepted, you are guaranteed lifetime employment (i.e., tenure). After all, someone has to interpret this thing to tell people when to plant each year, when to celebrate the religious festivals, etc.
Once we’ve decided on what cycles, we have to decide how to count them. Do we cycle through a small number of names (e.g., our months)? Do we make a fixed numerical count of cycles from some predetermined epoch (e.g., our years)?
Since most calendars have been either solar (based on the tropical year), lunar (based on the synodic month), or lunisolar (a combination of the two), let’s look at the problems we face making these cycles mesh.
Assume we take the day as the basic period (we don’t have to, but it makes sense, since it’s the light/dark rhythms that people base their activities upon). This means we need to fit the year and/or month cycles into some whole number scheme that approximates the observed values. As an approximation, we could round off the tropical year to 365.25 days and the synodic month to 29.5 days. These fractional days we can represent fairly easily, for the year by intercalating (inserting) one day every four years and for the months by making our lunar months alternate between 29 and 30 days.
With these approximations, we are only off the true period of the tropical year by about 1 day every 128.5 years, but with the lunar cycle it takes less than 3 years to slip a day (hence we?ll need to add some leap days here as well). Moreover, whether we use the true values or their approximations, there is no obvious way to get a whole number of lunar cycles into a whole number of solar cycles (in case we want a lunisolar calendar). The nearest rough approximation, and one that seems to have been a common early choice, is 365 days and 12 1/3 lunar cycles (also 365 days if we alternate 29 and 30 day months) per solar cycle.
A much better approximation, and one that we will see cropping up repeatedly, is the Metonic cycle, which observes that 19 tropical years are equal to 235 synodic months. Plugging in the actual lengths year and month to these numbers, we find 19 years = 6939.6018 days 235 months = 6939.68865 days which means this approximation has an error of only about 1 day every 219 years. This error value will change somewhat, of course, when we use the 19:235 ratio in a civil calendar, which contains its own approximations to the year length (see below, particularly the Julian calendar).
These considerations should also make it clear that just because a calendar doesn’t match up to the solar or lunar cycles exactly doesn’t necessarily imply that astronomers in that culture didn’t have a much better idea of what the true values were. In fact, there’s direct evidence to the contrary. A calendar must balance accuracy against simplicity, and once a calendar is well established in a society, changing it can be very difficult.
Early Historical Calendars
Overview
There are a variety of calendars that precede the one currently used in the west (the Gregorian) and which have some direct influence on it. Calendars that had no discernible impact (e.g., the Chinese, Indian, and Mayan calendars) are not discussed here.
The Egyptian Calendar

No extant evidence is known that describes the workings of the oldest Egyptian calendar (that of the pre-dynastic period).

We do know that it must have been lunar. Among other things, the hieroglyphic symbol for “month” shows a crescent moon (the first visible crescent of the new moon) over a star. Reconstruction of further detail has been attempted, but the argument remains controversial. Of greater interest for later chronology, particularly astronomical events, is the Egyptian civil calendar, whose existence seems certain by the fifth dynasty, and might, although the evidence is slender indeed, go back to the pre-dynastic period. There is also evidence for a much later, probably unconnected, lunar calendar. It does not, however seem to have been widely used. See Clagett and Parker for further details.
The calendar we know as the Egyptian calendar has no link to the moon at all, although it kept the old hieroglyph. In the Egyptian calendar, there were 12 months of 30 days each. The months each had three “weeks” of 10 days each. Between the end of the 12th month and the beginning of the first month of the next year were five epagomenal (extra) days, resulting in a fixed year of 365 days every year. This calendar, almost a quarter of a day shorter than the tropical year, constantly shifted with respect to the seasons.
For agricultural purposes, the seasons were determined not by the solar equinox or solstice, but by the heliacal rising of the star Sirius (Sothis in Egyptian), which roughly coincided with the flooding of the Nile. Every 1461 Egyptian years (1460 Julian years) the heliacal rising of Sirius came back around to its original position, a time known as the Sothic period. Early interpreters of the Egyptian calendar thought that the Egyptians actually maintained a separate calendar to track Sirius, but in the absence of any evidence, this position has been vigorously disputed by later scholars.

Originally, the months were simply numbered as a month of a season, rather than named. There were three seasons, each of four months. These names suggest that the seasons were originally intended to coincide with the Nile’s flooding (and probably did when the calendar was still lunar), but once the calendar took on the form we know they rolled through the seasonal year with the months. From the New Kingdom on, the months are often named.
Years were reckoned by pharaonic reign. For example, one actual Egyptian date appears as “Year 9 under the Majesty of the King of Upper and Lower Egypt Djeserkare. The Feast of the Opening of the Year III Shemu 9. The Going forth of Sothis.”
Since Djeserkare is a name for Amenhotep I, we can interpret this as “in year 9 of Amenhotep I, the heliacal rising of Sirius fell in the 3rd month of Shemu, day 9.”
This particular date is one of only a handful surviving that record the Sothis rising in terms of the civil year. It’s from the so-called Ebers Calendar, and in theory provides a good correlation of the civil calendar to Julina days. Unfortunately, a precise determination of when this fell is impossible. We don’t know where the observation was made or what the exact conditions of observation were (which would determine how many degrees above the horizon a star would need to be before being visible to the naked eye. A range of dates, however requires that it be some time in the 2nd half of the 16th century BCE.
In 238 BCE, during the reign of Ptolomy III, the Canopus decree ordered that every four years there should be 6, rather than 5 epagomenal days, in other words, a leap year. Egyptians were very resistant to this change, however, and the attempted reform seems to have failed. An effective implementation of this so-called Alexandrian calendar did not come until Augustus introduced it (25 BCE).
The Egyptian calendar had an importance well beyond its purely Egyptian use. Astronomers used the old Egyptian (not the Alexandrian) calendar throughout antiquity and the Middle Ages because its absolute regularity in the number of days in both the months and the year made calculations much easier. Such regularity was highly desirable, as antiquity had neither Arabic numerals nor even the concept of zero to make complex mathematics tractable.
The Babylonian Calendar

Babylonian astronomy plays a critical role in the development of Greco-Roman astronomy, which is in turn essential for establishing a reliable chronology of the ancient world. Among other things, it is from the Babylonians that we derive our sexagesimal system for minutes and seconds. We are very fortunate that we are in a position to confirm independently the chronology found in major works like the Almagest. Thanks to excavations of numerous cuneiform tablets we have abundant evidence of the Babylonian calendar, the regnal dates of their rulers, and their astronomical observations.

The Babylonian calendar was lunisolar, which means that periodic leap months were required to keep the lunar and solar years in synchronization. The months began at the first visibility of the new crescent at sunset. In later Babylonian times, the new moon was determined not by direct observation but by a complex mathematical rule, which in fact yielded a very close result.
The intercalary month was inserted either after Ululu or Addaru, and it was simply called Second Ululu, or Second Addaru. There is some evidence that by the reign of Nabonassar (747 BCE) Babylonian astronomers had discovered the Metonic 19-year cycle, but until the 4th century BCE, there is no evidence that a 19-year cycle was used to assign fixed intercalary years within the cycle. In its fully developed form, years 3, 6, 8, 11, 14, and 19 had a second Addaru, and year 17 had a second Ululu.
For earlier Babylonian history, years are reckoned by the regnal year of the ruler. After Seleucus I conquered Babylon, scribes began to record dates in the Selucid Era (SE), a continuous count of years that did not stop with the death of Seluceus. Year 1 SE corresponds to 312/11 BCE, a correspondence that can be confirmed by records of astronomical observations dated in this era.
After the Parthians conquered Mesopotamia, the western part of the Selucid empire switched the beginning of its year from spring (Nisanu) to fall (Tashritu), under Greek influence. The Parthians kept Nisanu as the beginning of the year.
The seven-day cycle makes its earliest appearance in Babylonian documents of the 7th century BCE. It is not quite yet the week as we know it, however. In origin, it seems to have been one fourth of the approximate time in a month the moon was visible. In short, it does not include the days around the new moon, and is not therefore a continuous cycle. To picture what this “week” was like, imagine one of our months with four regular weeks, and then a few epagomenal days at the end of the month, which do not belong to any week.
The Jewish Calendar

The Hebrew calendar looks much like the Babylonian one, and there is clear influence from the time of the Babylonian captivity. In its earliest stage, the months were numbered, rather than named. The names eventually adopted were versions of the Babylonian names. As in Babylonian reckoning, Nisan was originally the first month of the year. Tishri became the first month along with the western part of the Selucid empire, and it remains so today.

Despite this obvious Babylonian influence, Jews did not adopt the regular 19-year cycle for inserting intercalary months, nor did they use Babylonian mathematical calculation of new moon. The decision to insert an extra month was made by the Sanhedrin in Jerusalem on rather vague criteria such as the appearance of new plants. Because they measured neither the equinox nor helical risings, the old Hebrew calendar cannot be reconstructed by mathematical formula.
Another difference between the Hebrew and the Babylonian calendar is the treatment of the 7-day cycle. Recall that the Babylonians had a 7-day cycle, but the days around the new moon when it was invisible were not included. In the Jewish scheme, the 7-day interval between Sabbaths runs independently of the months and years. There are no epagomenal days. The days are numbered 1 to 7. Only the Sabbath, the seventh day, is named, although day 6 is sometimes called ereb shabbat, “the day preceding the Sabbath.”
In the 2nd and 3rd centuries CE, the Jewish calendar was reformed. The primary purpose of this reform was to regularize the intercalation of months and the length of the months. Using the Metonic cycle of 19 solar years, months are intercalated in years 3, 6, 8, 11, 14, 17, and 19 of the cycle, exactly the same spacing as in the Babylonian cycle. In a regular year, the months alternate between 30 and 29 days (Tishri has 30, Marheshvan 29, etc.). The embolismic month has 30 days, and intercalated between Adar and Nissan (never after Elul). It is called Second Adar, or Weadar. Nissan still has 30 days.
Certain customs about the days of the week upon which the High Holy Days may be celebrated require adding a day to certain years and then subtracting a day from the following year. The shorter years are called “defective”, and Kislev is decreased to 29 days. The longer years are called “perfect,” and increase Marshevan to 30 days. Those interested in the precise formulation of these rules should consult the references.
The epoch that Hebrew calendar currently uses, the Hillel world era, begins October 7, 3761 BCE. This epoch was calculated by Hillel II in the 4th century CE, but did not become universal practice until the end of the Middle Ages. Other epochs used before then were the so-called era of Adam (3760 BCE), and the Selucid (312 BCE).
The Ancient Greek Calendar

Of all ancient calendrical systems, the Greek is the most confusing. The Greek Calendar is much like ancient Greece itself. It shared a certain basic similarity from region to region, but each city-state kept its own version. All the Greek calendars were lunisolar and shared the same basic features of the other lunisolar calendars we’ve examined so far: twelve months, with a periodic intercalation of a thirteenth.
The Athenian calendar is the best known and most intensively studied, and I shall therefore use it as a model. The Athenian months were named Hekatombion, Metageitnion, Boedromion, Pyanepsion, Maimakterion, Poseidon, Gamelion, Anthesterion, Elaphebolion, Munychion, Thargelion, and Skirophorion. (For a list of the known month names in other Greek areas, see Ginzel, vol. 2, pp. 335-6). The intercalary month usually came after Poseidon, and was called second Poseidon. Hekatombion, and hence the beginning of the year, fell in the summer. Other Greek regions started their year at different times (e.g., Sparta, Macedonia in fall, Delos in winter).
For the historian inclined towards tidy orderliness, the regrettable fact is that the Athenians were simply unwilling to stick to a completely regular calendar, which makes reconstruction difficult. Their irregularity was not from lack of astronomical knowledge. In 432 BCE, the Athenian astronomer Meton instituted his 19-year cycle, fixing regular intercalations (whether Meton got this cycle from Babylonia or discovered it himself is not known). From that point, a small group of Greek astronomers used the Metonic cycle in their calculations, but this should be regarded as an astronomer’s ideal calendar. Abundant epigraphical evidence demonstrates that in the civil calendar, while the archons inserted approximately the correct number of intercalary months over the long term, the specific corrections were somewhat arbitrary, as the archons saw fit. This irregularity doesn’t really affect the long-term workings of the calendar, but it does make things very confusing when trying to establish a precise date for an event.
The Athenians seem to have taken a rather casual attitude towards their calendar. It appears they used neither a regular formula nor continuous direct observation to determine the length of the months. Most likely, they followed a general rule of alternating months (29 and 30 days long), subject to periodic correction by observation.
In addition to this calendar, which has been called the festival calendar, Athenians maintained a second calendar for the political year. This “conciliar” year divided the year into “prytanies,” one for each of the “phylai,” the subdivisions of Athenian citizens. The number of phylai, and hence the number of prytanies, varies over time. Until 307 BCE, there were 10 phylai.
After that the number varies between 11 and 13 (usually 12). Even more confusing, while the conciliar and festival years were basically the same length in the 4th century BCE, such was not regularly the case earlier or later. Thus documents dated by prytany are frequently very difficult to assign to a particular equivalent in the Julian calendar, although we are usually secure in assigning an approximate date. Since the prytany will play no role in my argument for establishing a basic chronology, I will not go into the intricacies here. The references cited below, however, go into the problem in mind-numbing detail.
Ordinary records of Greek city-states were dated according to the eponymous year of the person in power, be that the archon, king, priest of Hera, etc. For Athens, our list of archons from the 4th c. BCE to the later 1st c. CE is complete for all but a few years, which is a great help in verifying our chronology. Regional eponymous years, however, are awkward for historians trying to correlate the various areas, a problem no less evident to the ancient Greek historians than it is to us. The solution that seemed obvious to them was to reckon time by the intervals between Olympiads, in addition to giving eponymous years.
That the Olympics were held every four years is well known, but some evidence for that assertion is not out of place. Ancient writers all refer to the Olympics as a 5-year period (in Greek, pentaeterikoi, Latin quinquennales). This might seem strange, but Greeks and Romans most commonly counted inclusively; that is to say:

which we would call a four-year interval. NB: our way of counting implies a zero start, a concept both Greeks and Romans lacked. Since the Greek calendars all differed slightly, you might wonder how everyone managed to get to the games on time. The Pindar scholiast claims that for the early Olympiads, the festival was held alternately after 49 or 50 months, which is essentially equivalent to four years in a lunisolar calendar. This scheme makes perfect sense, because no matter what specific intercalary months the various cities did or did not decide to include, they could all simply count forward to 49 or 50. It also implies, by the way, that a rule of 8 years = 99 months was being used to determine this interval (although not that every Greek city used this formula for their own intercalations).
Since the Olympiad was a summer festival, it was eventually correlated to the Attic (Athenian) calendar, so as to begin on Hekatombion 1, which might imply a certain agreement about when intercalations should be added, or simply indicate Athenian cultural dominance.
Ancient historians date by Olympiad by giving both the number of the Olympiad and the year within the cycle, 1-4 (the Olympiad itself was held on year 1). Additionally, lists of Olympic winners were maintained, and the 3rd c. BCE writer Timaios compiled a synchronic list comparing Olympic winners, Athenian archons, Spartan kings, and the priests of Hera from Argos.
Olympiad 1,1 correlates to 776 BCE. We do not actually need to believe an actual festival was held on this date, but when Greek historians are writing in later times, they date their own events using this as the epoch. We can establish a precise correlation to the common era from a variety of different sources, but the most definitive comes from a passage in Diodorus, where he dates the year of a total solar eclipse to the reign of the Athenian archon Hieromnemon, which he also gives as Ol. 117,3. The only astronomically possible date for this event is August 15, 310 BCE, which fixes our epoch.
One thing to be wary of with reckoning by Olympiad is that writers calculated the start of the year by their local convention (spring, summer, winter, or fall). For example Ol. 1,1 correspond to Fall, 777 – Fall 776 BCE by Macedonian reckoning. Byzantine writers who use Olympiads take the year to begin on September 1.
Most of the other eras used by Greek writers are of little importance. One worth mentioning, however, is the Trojan Era (from the destruction of Troy), which is found in a number of historians’ works. This date, of course, is purely conventional, and can be seen as analogous to the various world eras (e.g., Hillel’s above). A wide variety of starting points are found, but the one with the widest currency, developed by Eratosthenes, set it 407 years before the first Olympiad (1183 BCE).
The Roman Republican Calendar

The very earliest calendar used by the Romans is obscure. By later Republican times, however, it is, if not regular, at least well documented. From the time we have direct evidence of it, the pre-Julian calendar was roughly lunisolar. Certain Roman religious customs, as well as the monthly subdivisions of Kalends, Nones, and Ides, indicate that the calendar was originally lunar, and that months began upon direct observation by a priest of the new moon.

There were 12 months in an ordinary year, but many of the months were shorter than they are now. Their Latin names will largely look familiar. A regular year thus had 355 days. The lengths of the months indicate that by the time of our earliest records the year was not measured by direct observation, as no month so measured could have 31 days, but by conventional rule.
The number-names of the last six months indicate not, as is sometimes said, that there were originally 10 months (a number that if true would yield a nonsensical year length), but that the year originally began in March. There is a fair amount of confusion in different accounts of the Roman calendar about the beginning of the year. Sometimes it will be said that the year began on March 1 until Julius Caesar reformed the calendar. This theory was disproved by the excavation of an actual republican calendar in the 1920s, which clearly shows the year started in January. It is also sometimes said that the beginning of the year changed in 153 BCE, but in fact what happened this year was that the time when consuls took office was synchronized with the calendar year. January seems to have become the beginning of the year when the republican calendar was introduced, but there is so little information about that reform (taking place, it appears, in the 5th-century BCE) that we can say little more.
To keep the calendar roughly in line with the seasons, a leap month (it had no name other than “the intercalary month”) was inserted at the end of February. This position, which falls more or less at the end of the year when the year began in March, implies that the intercalary month predates the change in observation of the new year. The decision to insert the intercalary month was made by the pontifexes. In theory the intercalation was roughly every other year. In practice, pontifexes seem to have been rather lackadaisical in carrying out their offices, and the calendar was sometimes allowed to get drastically out of synchronization with the seasons. Roman intercalation was peculiar. February was reduced to either 23 or 24 (it varied from year to year), and a 28-day month was added afterwards. This peculiar habit was a result of the ways that days of the month were counted in the Roman system.
There were two important festivals, Refugium and Equirria, which fell at the end of February and which could not be separated from the beginning of March. They are transferred to the intercalary month, but notice with the Roman method of counting backwards, they keep their day numbering constant whether it’s a regular or intercalary year. Note that our general conversion rule applies for intercalary years as well. If February has 23 days, February 15 = a. d. x Kal. intercal. (xi if Feb. has 24).
The Roman calendar also had a recurring cycle of 8-days, similar to our week, called the nundinae = nine-days (once again, we have that habit of inclusive counting). This “week” was not religious in significance, but originally indicated days upon which a market would be held in Rome. Extant Roman calendars indicate this interval by giving each consecutive day a letter A through H. Note that this was simply a mnemonic marker. They did not call them “day A,” etc. The 7-day week and its names were not introduced into Roman civil life until the imperial period.
While dating by Olympiad was occasionally used, Roman writers most often reckoned years by the eponymous names of the consuls in office that year. This habit persisted through the imperial period as well, even though (excepting those occasions when the emperor was also consul), consular power was much reduced. An unbroken list of consuls from the founding of the republic (conventionally, 509 BCE) through the late empire survives. Some have questioned whether all the earliest names in this are historical, but the later ones certainly are, and provide many opportunities for correlation to the Common Era.
The so-called Varronic Era, named for the late Republican antiquarian Marcus Terentius Varro, was only rarely used during the Republic, but became more popular under the emperors. In it, years were dated from the founding of Rome, or AUC (ab urbe condita), which was correlated to the Greek reckoning by saying that it fell in Olympiad 6,3 (olympiadis sextae anno tertio), i.e., 753 BCE. Like most eras calculated from a foundational date in the distant past, the Varronic Era should be seen as purely conventional. That is, even if Rome wasn’t founded in 753 BCE, dating in this system can still work just fine, as long as it remains consistent.
The Julian Calendar

The Julian calendar was a modification by Julius Caesar of the Republican calendar. As pontifex maximus, Caesar was responsible for the smooth operation of Rome’s calendar, which previous neglect had allowed to fall behind the seasons. In the second year of Caesar’s dictatorship (707 AUC = 47 BCE) the calendar was running seriously behind the solar year. Some scholars have argued it was 90 days behind, and Caesar began by ordering an ordinary (pre-Julian) leap year (with the extra month). Be that as it may, during his second consulship, 708 AUC, he inserted 67 days (exactly how isn’t perfectly clear, but probably 2 months between November and December of 22 and 23 days, plus another intercalary month after February). So by the end of the year 708 (46 BCE), the calendar was pretty much back in sync with the seasons. As you might guess, these changes caused a great deal of confusion at the time. Later writers called it the annis confusionis.
In 709 AUC (45 BCE), the real Julian calendar begins. Not only did Caesar decree the leap year rule, but he lengthened several months by putting 10 more days into the regular year. The new leap day was inserted exactly where the old leap month was, i.e., after the 24th of February. Both the 24th and the leap day were counted as vi Mar., the second was called bis vior the bisextile.
The Julian calendar was a modification by Julius Caesar of the Republican calendar. As pontifex maximus, Caesar was responsible for the smooth operation of Rome’s calendar, which previous neglect had allowed to fall behind the seasons. In the second year of Caesar’s dictatorship (707 AUC = 47 BCE) the calendar was running seriously behind the solar year. Some scholars have argued it was 90 days behind, and Caesar began by ordering an ordinary (pre-Julian) leap year (with the extra month). Be that as it may, during his second consulship, 708 AUC, he inserted 67 days (exactly how isn’t perfectly clear, but probably 2 months between November and December of 22 and 23 days, plus another intercalary month after February). So by the end of the year 708 (46 BCE), the calendar was pretty much back in sync with the seasons. As you might guess, these changes caused a great deal of confusion at the time. Later writers called it the annis confusionis.
In 709 AUC (45 BCE), the real Julian calendar begins. Not only did Caesar decree the leap year rule, but he lengthened several months by putting 10 more days into the regular year. The new leap day was inserted exactly where the old leap month was, i.e., after the 24th of February. Both the 24th and the leap day were counted as vi Mar., the second was called bis vior the bisextile.

In adding the new days to the calendar, Caesar tried to disturb the separation between festivals as little as possible (relative to the Kalends system of dating), and the new days were actually added just before the last day of each month that was extended, except for April, where it was inserted between the 6th and 5th Kalends. The month of July (Julius, from earlier Quinctilis) got its name in 44 BCE by decree of the senate. Notice that while our general rule for converting days of the month still applies, the Kalends numbering in the lengthened months is different in the Julian and Republican calendars. E.g., December 25 = vi kal Jan. in the Republican, but viii kal. Jan. in the Julian.
Because the pre-Julian Roman calendar was not regular, the custom of historians is to use the Julian calendar proleptically for earlier dates. That is, dates before 45 BCE, which are naturally recorded in different calendars, are translated into the Julian calendar. This convention explains one seeming paradox: the first year of the Julian calendar should have been a leap year in the new sense, but one was not celebrated that year. Thus the Kalends of January that year actually fell on January 2, 45 BCE.
After Caesar’s death, his new rules were faithfully followed. Unfortunately, the new pontifices do not seem to have understood his rules quite as they were intended. Caesar specified a leap year at four-year intervals, and since Romans typically counted inclusively (see the remarks on Olympiads), they took this to mean every three years. So leap years were observed in 42 (712 AUC), 39, 36, 33, 30, 27, 24, 21, 18, 15, 12, and 9 BCE. At this point, someone must have brought the problem to Augustus Caesar’s attention, because he decreed that there should be no leap year at all for the next 12 years, and carefully rephrased the rule to say “intercalate at five year intervals,” so dense Romans would get their counting right. The first correctly observed leap year was in AD 8. Augustus also took the opportunity to rename the month Sextilis after himself at the same time, which is how we wound up with August, but there is no evidence to support the story that he lengthened that month so that it would not be inferior to Julius’s month. In fact, as indicated above, the month lengths were all changed by Julius Caesar.
Start of the Calendar Year
The Romans took the start of the year to be January 1, just as we do. In examining other documents, however, particularly medieval ones, we need to be aware that such was not always the case. In the Byzantine empire, September 1 was the beginning of the new year. In the West, January 1 persisted, but alongside of that you also find year the beginning on December 25, March 25, or even Easter. Most of the early Western reluctance to use January 1 as the year’s beginning stemmed from Christian disapproval of the traditional pagan ceremonies held on January 1. It is commonly thought that the institution of the Feast of the Circumcision was at least partly intended to give people a Christian holiday to celebrate on the first of January. Curiously, the calendars and tables the Church used to calculate Easter generally began in January, a tradition stretching back to antiquity. Eventually, January 1 regained its predominance in most of Europe. England persisted in using March 25 as the official new year until adopting the Gregorian calendar in 1752. Hence, a January-March 24 date will be look like it’s a year before. That is, the day after, March 24, 1715 in Britain is March 25, 1716. Many private individuals in England, however, persist in calling January 1 the New Year (see, for example, Pepys’s diaries).
Problems with the Julian Calendar

The Julian calendar was a major improvement over the older Roman calendar. The rule for leap years was simple enough that anyone could keep track of it, and the calendar stayed pretty much in time with the solar year. But just how accurate was the Julian calendar? With the quadrennial leap year, the mean calendrical year is 365.25 days. As we have seen, the actual length of the mean tropical year is closer to 365.2422 days. So the civil year on average is too long by about 11 minutes. Over a long period of time, this discrepancy means the seasons will slowly fall behind the calendar date. If we calculate a value Y, which equals the number of calendar years it takes for one day of “seasonal slip” to occur, we have a way to compare the relative accuracy of various calendars.
For those interested, the rough formula is Y = 1/(MCY – 365.2422), where MCY is the mean civil year length in days. To even more precise, we could take into account the gradually decreasing length of the tropical year. That requires we consider the calendar over a specific span of years and replace the approximate value for the tropical year with: 365.24231533 – (y1 + y2) * 3.06713e-8, where y1 is the start year and y2 the stop year in astronomical years (= Common Era, but for BCE dates, use negative number and add one, e.g., 1 BC = 0, 2 BC = -1, etc.). This kind of precision will be irrelevant unless we have precise astronomical observations in the relevant years against which to compare it. Otherwise, rounding the number to the nearest 10th gives a good value for comparison.
A similar value, M, could be generated to show the number of months it takes for a lunar calendar to slip 1 day, assuming the calendar works by rule rather than direct observation.
In the Egyptian calendar, Y = 4.1; clearly, no one who used this calendar was seriously concerned to keep it aligned with the seasonal year. Using the approximate formula, Y for the Julian calendar is 128.2; the precise formula, considered over the span -44 to 1582, gives 129.3.
These numbers should suggest why the Julian calendar remained unreformed for so long. Within any one person’s lifespan, only an astronomer would notice the difference. Even if a culture keeps records over a long period of time, the change is not all that great: less than 8 days in a millennium. While an extremely long period of time (about 27,700 years) might change “the darling buds of May” into the darling buds of December (in the northern hemisphere, of course), it hardly seems like a pressing problem.
The fact is, however, that from the beginning of the 13th century, there was a constant call among leading intellectuals (most notably Roger Bacon in 1267) for a modification to correct this drift. The press of other urgent matters and general inertia delayed matters until the late 16th century, but eventually a change was made. To understand why, we first need to look at the calculation of Easter.
The Calculation of Easter
Overview
In his Ecclesiastical History of the English Language, the eighth-century historian Bede repeatedly mentions the controversy between the Irish and the Roman churches over the correct calculation of Easter. As Bede sees it, the culminating moment in this battle comes at the synod of Whitby when both sides present their arguments before King Oswy, who decided in favor of the Roman method. From our distance, the argument may seem rather silly—an argument over how many angels can dance on the head of a pin. (The standard answer to that question, by the way, is “as many as God wants.”) Looking more closely, we might notice that beneath the surface debate is really a question of power—who gets to define the rules for the most important Christian celebration. In any event, for the historian interested in establishing a chronology of the Middle Ages, the debate over how to calculate Easter is invaluable. We owe the AD system of counting years to an early Easter calculator, and the Church’s continuing concern that Easter be celebrated correctly ensured that various regions all adopted the same count of years—the one we still use today.
Easter in the Early Church

From at least the 2nd century CE, there was prolonged controversy over what date upon which the passion of Jesus ought to be celebrated. Much of the confusion stems from ambiguity in the biblical account. All four gospels clearly state that Jesus rose from the grave on the first day of the week (now called Sunday), three days after the crucifixion. They also, however, refer to the Last Supper with relation to Passover, which begins on Nisan 15. The synoptic gospels imply it was a Passover meal, but John says it was on the day before Passover (Nisan 14).
I won’t go into the doctrinal disputes to which these ambiguities gave rise. The interested reader should consult the “Easter” entry in a good encyclopedia of theology (e.g., the Dictionnaire de Théologie Catholique). The generally favored solution was that Easter should always be on a Sunday, and that there should be some rule for determining a time fairly close to Passover. Just what this rule should be took a long time to hammer out. Relying upon the Jewish definition of Passover was uncongenial to many Christians, and as the Jewish calendar was not yet fixed by rule there was also the practical problem of waiting for the determination of the Sanhedrin in Jerusalem for a date which then had to be transmitted to widely separated churches throughout the Roman empire. To calculate Easter, then, Christians needed to find a lunar month in spring, which required both a definition exactly when spring began and a method of computing lunar months (i.e., a lunar calendar) that could be converted into the Julian calendar.
The rule eventually agreed upon was that Easter should be celebrated on the Sunday after the 14th day of the “Paschal” month. That Paschal, or Easter, month (essentially a Christian version of Nisan) is the one where the 14th day is on or next after the vernal equinox.
Even after this definition was generally accepted, there were still problems. When, exactly is the vernal equinox, and what sort of lunar calendar does one keep to track the Paschal month?
The Romans took the vernal equinox to be on March 25, a traditional date, to which they clung stubbornly for many years. Many of the eastern churches, however, took March 21 as the equinox. This measurement was fixed by direct observation of astronomers in Alexandria in the early third century. During that time, Alexandria was famous as a center of astronomic knowledge, and it was a natural place to go for expert consultation.
The lunar calendar used to track the new moons was also a subject of debate. The earliest surviving Easter tables show that the approximation 8 years = 99 months was used. This approximation results in an error of 1 day every 5.2 years. Clearly, for any long-term calculation of the moon, this rule will very quickly accumulate significant errors. In the early third century, a Roman named Augustalis introduced a new approximation: 84 years = 1039 months. This equation leads to an error of 1 day every 64.6 years—a significant improvement. Meanwhile the eastern churches, undoubtedly advised by Alexandrian astronomers, had found an even more accurate cycle: the familiar Metonic equation of 19 years = 235 months. This approximation has an error of only 1 day in 316.6 years.
Alexandrian Easter

In 325 CE, the Council of Nicaea met. One of its primary tasks was to ensure a uniformity of observation in liturgical matters, particularly with respect to the observation of Easter. The council decreed that Easter should be kept on the same day everywhere, and from the evidence of a surviving letter, it seems that the Alexandrian church was to make the standard calculations. Just because the Alexandrian church was tasked with calculating Easter does not mean they continued to rely upon astronomers to supply them with the actual date of the vernal equinox. Rather, they seem to have taken a number from the astronomers sometime in the 3rd century, and simply used it from then on. In 325 CE, for example, the equinox fell on March 20 (in Alexandria).
Rome did not actually abandon the 84-year cycle or March 25th equinox (which, of course, led to periodic differences in date between the Alexandrian and Roman churches), but often Rome seems to have accepted Alexandrian calculations. Not always, however. From time to time, the Roman church expressed its unhappiness with dates that it considered unsatisfactory. Ironically, every time the Romans consulted experts, they were essentially told that their way was inaccurate, and that they should adopt the Alexandrian computation.
The Start of Anno Domini Dating

In one of these periodic reexaminations of the issue, the problem was handed over to one Dionysius Exiguus (Denis the Little, or as I like to call him, Denis the Scrawny). Dionysius reported back reaffirming the Alexandrian method of calculation, and since the tables currently in use were about to expire, he also took the opportunity to calculate the dates of Easter for the next 532 years. The tables he produced and the introductory letter have survived. To the beginning of his tables he prefaced the last 19 years of the old tables. Those tables identified the year in the year of Diocletian (sometimes called the Era of the Martyrs, for the great persecutions of Christians that took place under that emperor), years 228-247 to be precise. When Dionysius continues his table, however, he dates the years in the cycle from the incarnation of Christ (anno domini is Latin for “year of the lord”), as he believed them to be. In his letter, he explains that he preferred that Jesus, not a persecutor of Christians, be remembered in his tables. The first year in his continuation is 532, which is thus equated with the year of Diolcetian 248. To provide another correlation to a known count of years, Dionysius also indicates the year of the indiction, a 15-year cycle used in the late Roman empire for purposes of taxation. AD 532 was the 10th year of the indiction, according to Dionysius.
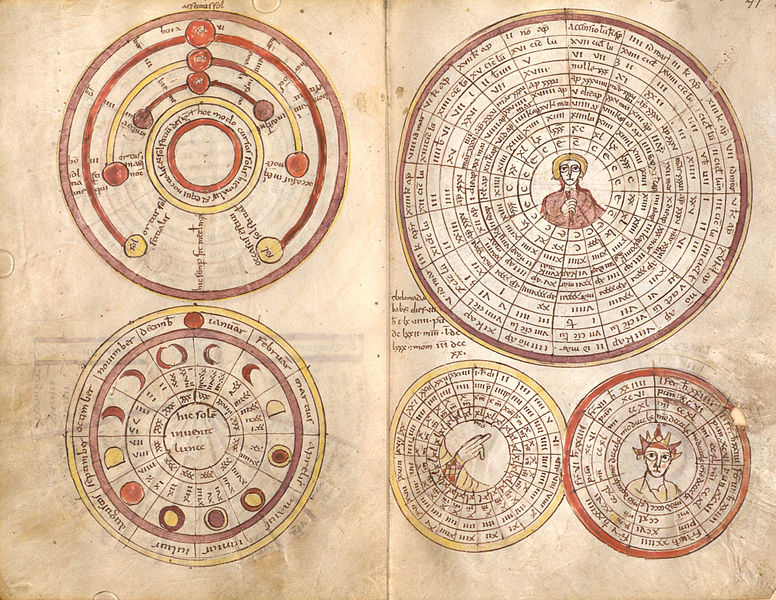
A Medieval Easter Table

Let’s start with the column headings, which in this case actually come in the middle of the table. Expanding the abbreviations, the headings mean: anni domini (years of the lord); indictiones(indictions); epactæ (epacts); concurrentes; cicli lunae (lunar cycles), 14ma Luna(the 14th moon); dies dominica post (the Sunday afterwards); luna ipsius (this moon).
The indiction we have already seen. It plays no direct role in the calculation of Easter, but note that the cycle remains consistent with that given by Dionysius. The epacts indicate the age of the moon (i.e. days into the lunar month) on March 22, the earliest possible date of Easter Sunday. The concurrentes give the day of the week (the so-called ferial numbers) of March 24th. The lunar cycles track the Metonic, 19-year cycle. Later in the Middle Ages, this cycle will be determined by the numerus aureus, the golden number, so called because it is the key to figuring out the date of Easter. Note, however, that this lunar cycle, while it has the same practical effect as the golden number, is not exactly the same. For example, 1010, which has a golden number 4, is listed as the first year of the lunar cycle. The 14th moon is the 14th day of the lunar month, i.e., the full moon. The Sunday afterwards is Easter. The “moon itself” is the age of the moon, i.e., the day of the lunar month, on Easter.
Apart from the numbers and dates, the other abbreviations in the margin are B, for bisextilis, i.e. a leap-year; END for endecadas and OGD for ogdoadasmark the subdivisions of the Metonic cycle. The first is a period of 11 years, the second of 8. They coordinate the insertion of lunar leap.

If you check these years (for example with the ChurchCalendar applet) you will find only one (March 17) is wrong. This one is an obvious scribal blunder. Easter must come after the full moon. The scribe wrote 16 Kalends of April when he should have written 16 Kalends of May, which is April 16, the correct date. Further, if you calculate the week day of the 24th, you will find that all of them match up correctly (1 = Sunday, etc.).
The Gregorian Conversion

In 1582, Pope Gregory XIII decreed a modification to the Julian calendar. The reform consisted of a one-time correction in the date (skipping some days in the calendar) along with some tweaks to the rules of the calendar itself. For the civil calendar, the only substantive change was to omit 3 leap days every 400 years (in years evenly divisible by 100 but not 400, e.g., 1700, 1800, 1900, but not 2000). There were also changes to the way that the age of the moon was calculated for the purposes of finding the date of Easter. Considered as a theoretical calendar (i.e., projecting it back before it was actually invented), the Gregorian calendar matches up with the Julian in the third century CE.
From a seasonal point of view, a the difference between the Gregorian and the Julian calendar wasn’t yet really all that pressing a matter, only 10 days in 1582, only 14 days in the twentieth century. The logical question thus becomes, why did it matter? The short answer is religion, which is, in most cultures, very concerned with keeping time. For Christianity, the fundamental chronological problem was the calculation of Easter, and this difficulty drove the reform. Recall that Easter is supposed to be the first full moon after the spring equinox. But as Easter was calculated by rule, not astronomical observation, the slip of the equinox meant that the rule was badly in error. The Gregorian calendar was designed to restore the spring equinox to the March 21 date that had been traditional since the Council of Nicaea.
Most countries adopted the Gregorian calendar in a single, one-time correction. Catholic countries quickly adopted the reform when Pope Gregory proclaimed it. Many of the major countries (Italy, Spain, Portugal, Poland), skipped from Thursday, October 4, 1582 to Friday, October 15, 1582, which we now take, for simplicity’s sake, to be the canonical point of switch. Notice that the day-of-the-week cycle is not altered in the switch (October 15, 1582 would have been a Monday in the Julian calendar). The reformers wanted to preserve the seven-day cycle unaltered, as they believed it was biblically ordained. The other Catholic countries quickly followed suit. Some, like France, by the end of 1582, others, like the Catholic parts of Switzerland (and, interestingly, the Spanish colonies in America—probably the result of delays in communication—waited until 1584. For some odd reason, the Spanish Netherlands switched over at the very end of 1582 (from December 21 to January 1), which means they skipped Christmas that year. (The October time was originally picked to omit as few feasts as possible from the church calendar, and Christmas seems a doozy of a feast to skip.)
In an age of intense religious passion, the simple fact that the Pope instituted the reform was enough to make Protestant countries reject the change. The greater part of protestant Germany did not switch to the Gregorian calendar until 1700, the Protestant Cantons of Switzerland and Protestant Netherlands until 1701.
The Swedish dithered. In 1700 they began what was intended to be a gradual switch to the Gregorian calendar. They planned to stop observing leap years until their calendar was in line with the Gregorian one. They did omit the leap year in 1700, but observed the leap year in 1704 and 1708 (apparently they forgot the plan). Thus they were 10 days out of step with the Gregorian calendar and 1 day off from the Julian. Then, in 1712, they changed their minds, and went back to the Julian system by adding two leap days to February. Somewhere in Sweden, there are probably some unique baptismal records of people whose birthday was on a date never to be seen again: February 30. Lithuania and Lativia, which were under Polish rule at the time of the reform (and hence changed in 1582), actually reverted to the Julian calendar, so strong were the feelings. They did not change back again until the 20th century.
Although Queen Elizabeth I initially expressed some interest in changing the calendar in 1582, the Church of England effectively tabled the idea, which was not taken up again for nearly 170 years. By that time, passions had sufficiently cooled that when the idea was introduced as an act of Parliament in 1752, it passed with hardly a murmur. The English colonies in America changed at the same time. By that time, 11 days now had to be added, which the English did by skipping from September 2 to September 14, 1752.
In some areas of Europe, there were riots when authorities tried to introduce the Gregorian calendar (in the 16th century), but the notion that there was popular discontent in England over the shift seems to rest entirely upon a William Hogarth print, which shows a mass demonstration through a window, with the protesters holding up the famous banner saying “give us back our 11 days.” Contemporary newspapers and other records, however, give no such indication, although there are some surviving sermons that indicate the authorities took pains to explain the situation carefully so that there should be no misunderstanding. The entire idea probably rests on Hogarth’s rather jaundiced view of lower-class ignorance, rather than historical reality.
In 1753, Sweden finally caved in, following Great Britain’s lead.
The last Christian countries to accept the Gregorian calendar were the Orthodox ones. Many (those under Russian domination), did not do so until the Bolsheviks decreed the change in 1918 (the October revolution actually took place in November, according to the Gregorian calendar), although there was a history of failed attempts at reform in the 19th century. The Greeks didn’t switch over until 1923.
Bibliography
- The Alternative Service Book 1980: Services authorized for use in the Church of England in conjunction with The Book of Common Prayer together with The Liturgical Psalter. (1980).
- The Book of Common Prayer and Administration of the Sacraments and other Rites and Ceremonies of the Church Together with the Psalter or Psalms of David According to the use of The Episcopal Church. (1979).
- Bonniwell, William R., o.p. A History of the Dominican Liturgy, 1215-1945. (1945).
- Brightman, F. E. The English Rite. Being a Synopsis of the Sources and Revisions of the Book of Common Prayer. 2 vols. 2nd ed, rev. (1921).
- Bushwick, Nathan. Understanding the Jewish Calendar (1989).
- Clagett, Marshall. Ancient Egyptian Science: vol. 2, Calendars, Clocks, and Astronomy (1995).
- Eisenberg, Azriel. The Story of the Jewish Calendar. (1958).
- Farmer, David Hugh. The Oxford Dictionary of the Saints. 3rd ed. (1992).
- Ginzel, F. K. Handbuch der Mathematischen und Technischen Chronologie. 3 vols. (1906, 1911, 1914).
- Gregorian Reform of the Calendar: Proceedings of the Vatican Conference to Commemorate its 400th Anniversary 1582-1982, eds. G. V. Coyne, S. J., M. A. Hoskin, and O. Pedersen (1983).
- Hatchett, Marion J. Commentary on the American Prayer Book. (1995).
- Missale ad usum percelebris ecclesiæ Herfordensis. (1874).
- Hughes, Andrew. Medieval Manuscripts for Mass and Office: A Guide to their Organization and Terminology. (1982).
- Jacobus de Voragine. The Golden Legend: Readings on the Saints. Trans. William Granger Ryan, 2 vols. (1993).
- Jasper, R. C. D. and Paul F. Bradshaw. A Companion to the Alternative Service Book. (1986).
- Johnson, Cuthbert, o.s.b., and Anthony Ward, s.m. Missale Romanum anno 1962 promulgatum. (1994).
- Michels, Agness Kirsopp. The Calendar of the Roman Republic. (1967).
- Mommsen, C. M. T. Römisches Staatsrecht, 3 vols. 3rd ed. (1887; reprt. 1952).
- Neugebauer, O. A History of Ancient Mathematical Astronomy. 3 vols.
- Meritt, Benjamin D. The Athenian Year. (1961).
- Parker, Richard. Calendars: The Calendars of Ancient Egypt. (1950).
- Parker, Richard A. and Waldo H. Dubberstein, Babylonian Chronology 626 BC – AD 75. (1956).
- Pinches, T. G., J. N. Strassmaier, and A. J. Sachs. Late Babylonian Astronomical and Related Texts. (1955).
- Pritchett, William, and Benjamin Meritt. The Chronology of Hellenistic Athens. (1940).
- Pritchett, W. and O. Neugebauer. The Calendars of Athens. (1947).
- Procter, Francis and Christopher Wordsworth. Breviarum ad usum insignis ecclesiae Sarum. 3 vols. (1879, 1882, 1886).
- Van Goudoever, J. Biblical Calendars. (1959).
- Weyns, N. I., ed. Sacramentarium Praemonstratense. (1968).
- Zeller, Chr. “Kalender-Formeln”, Acta Mathematica v. 9 (1886-7), pp. 131-6.
Originally published by Polysyllabic under the terms of a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 United States license.






