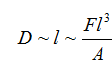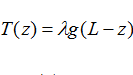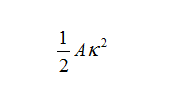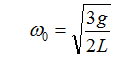Lecture by Dr. Raymond E. Goldstein at the Museum of London / 11.09.2016
Schlumberger Professor of Complex Physical Systems
University of Cambridge
Introduction
How do physicists and mathematicians think about hair? Everyone, especially those with their own hair, has surely been fascinated since their youth with the magical properties of bundles of hair: its “body” and “bounce”, how it moves in the wind, and its sheen. Scientists are not immune to the attractions of hair, and there are many areas within mathematics, physics, and even computer science in which you will find active research programs on this subject. For example, one of the great challenges of modern computer graphics is accurate rendering of moving hair. This is a difficult problem because of the need to deal with the behaviour of perhaps thousands of individual filaments, each with its own complex dynamics, and yet the collective properties of bundles are not easily deduced from those of the individuals.
I want to tell a scientific story about how questions that arose in an industrial research context about the properties of hair motivated a group of physicists and mathematicians to study this issue from a novel perspective [1]. Besides the intriguing mathematical issues involved, I think that this story provides a very good lesson in how basic and applied research can interact.
An invitation
Some years ago I received an email from the research and development unit of Unilever, the giant corporation that specialises in personal care products, asking if I would be interested in assisting them with their research on “hair array statistical mechanics”. Statistical mechanics is the study of the macroscopic properties of large numbers of particles, and so I could imagine what the writer meant by this research, but I had never known this particular subject was a field of study. For a moment I even thought this was an email scam! But through visits to the Unilever lab in Port Sunlight I learned about their interest in how the properties of hair bundles were affected by shampoos and conditioners, and their desire to use ideas from physics to improve these products. Of particular interest was the phenomenon of hair tangling, the familiar appearance of `knots’ in hair as it is combed. It is clear that this process depends sensitively on the curliness or waviness of hair, and it was this feature that was hard to describe mathematically. As we were grappling with a way to get into these kinds of questions, and examining standardized `switches’ of hair used in the industry, I suggested that we try first to understand the shape of a ponytail.
Physics and Mathematics of Hair
Drawings of Hair, From Hooke’s Micrographia (1665)
Each of us has 50,000-100,000 head hairs, the microstructure of which is rather complex. There is an outer layer, the cuticle, with a scaly structure, and a hierarchy of ever smaller inner structures culminating in the fundamental building blocks – the protein keratin- whose individual molecules are some nanometres in size. Hairs typically grow on the order of a centimetre/month, a rate which translates into the amazing speed of about 4 nanometres/sec. Some of the earliest microscopic images of hair were exhibited by Robert Hooke in his Micrographia (1665), in which he showed that hairs are typically round in cross section, without the central hole found in plants, for example, and they often have split ends.
There are three fundamental properties of hair that we shall consider when trying to explain the shape of a ponytail. Hair of course has mass, and it is convenient to use the mass per unit length λ. The worldwide average diameter d of hair is about 80 microns, about 1/12th of a millimetre, and its density is like that of wool, about 1.3 g/cm3, which translates into λ ~ 65 micrograms/centimetre, or, more intuitively, 6.5 grams/kilometre. If we have 100,000 hairs on our head and each is 0.25 m in length, we have 25,000 metres or 25 kilometres (and about 160 grams) of hair!
Second, hair has elasticity, which means that the individual fibres resist bending just like a piece of wood or steel. Of course, as they have a very small diameter the stiffness is extremely small. In general, we quantify the stiffness of a slender object by imagining it is clamped horizontally at one end and a force F is applied to the free end, deflecting it downward. The principles of elasticity theory show us that the filament acts like a spring in the sense that the deflection D is proportional to F, through the relation D~FL3/A, where L is the length of the filament and A is a property known as the bending modulus. The very strong length dependence in this relation is familiar to us all; it is harder to bend a short rod than a long one. In this relationship I have left out all constants of proportionality, emphasizing how the fundamental quantities of the problem enter. This is a very important aspect of mathematical analysis known variously as a `scaling analysis’ or `dimensional analysis’.
Hair has a complex structure
Now we can use this scaling law to decide how long a hair has to be for gravity to deflect it. If you hold a single hair horizontally between your fingers you can see that if the free length of hair is below, say, a few centimetres, it is unaffected by gravity, but if the length is 10 cm it surely bends. To understand this quantitatively, we make what is called a ‘self-consistent’ argument in which we seek the characteristic length for gravitation-induced bending. Surely an object is strongly bent if the deflection is of order its length, so we write
and then note that the gravitational force is the total mass, , times the gravitational acceleration, g=980 cm/s2. Thus,
This is a `self-consistent’ relationship in which the unknown appears on both sides of the equation. Solving for we find
Using the known value of the bending modulus, which is like that of a piece of nylon, we find ~ 5 cm, consistent with our experience. This is the first example of how simple physical reasoning can be used to understand basic properties of hair. As we know from elasticity theory that the bending modulus scales with hair diameter as and simple geometry tells us that we learn that increases with d as .
Rapunzel
This brings us to an important point in mathematical sciences. When we consider a physical quantity such as the mass of an object or its speed, it is not possible to make an absolute statement that it is large or small, because the obvious question is ‘Compared to what?’ Only pure numbers can be said to be large or small, and that is by comparison to 1. To decide whether from the point of view of gravitational forces hair is long or short it is natural to form the ratio of the total length to our characteristic length above. And as it is customary in mathematical sciences to name such pure numbers in a way that reflects either their discoverer or populariser, we declare the ratio to be the Rapunzel number, denoted by the symbol. When < 1 hair is short and stiff, unaffected by gravity, whereas when (say, at least or so) hair bends strongly under gravity. The switch of hair I show in the lecture has L=25 cm, and.
Hence, we introduce the “Rapunzel number: ![]()
The fact that hair has mass implies that when it hangs down approximately vertically there is internal tension that varies along its length. At any given point measured down from the top along the fibre the tension is just the gravitational force on the mass of hair below that point, so
so T(z) is maximum at the top and zero at the bottom.
Hanging hair is under tension
The last aspect of hair of relevance to our goal is its intrinsic waviness. This of course varies enormously from one person to the next, and even among the hairs on a given head. We say that this is ‘intrinsic’ curvature in the sense that it is not a consequence of external influences, although of course we can alter the shapes of hairs through thermal or chemical treatments. In the lecture I show examples of the random waviness of hairs. The mathematical problem of addressing the random shapes in a bundle of hair is one of a broad class of problems involving randomness in physical systems. It is often the case that one can make progress by separating out the effects of the average properties of the constituents from the contributions arising from deviations from the mean.
Leonardo, Euler, and Bernoulli
In the Notebooks of Leonard da Vinci we find a discussion “On the proportions and on the movements of the human figure”. Accompanying this is a drawing of the patterns of turbulent water flowing past the supports of a bridge, and Leonardo notes: “Observe the motion of the surface of the water which resembles that of hair, and has two motions, of which one goes on with the flow of the surface, the other forms the lines of eddies”. Here Leonard has anticipated the partitioning of effects described above, with eddies playing the role of deviations, and also a wonderful analogy between the alignment of hairs and the streamlines in a fluid. We shall use this idea to understand how randomness determines the energy of a bundle of hair.
The basic idea is to say that at every point within a ponytail there are two quantities of interest; ρ, the average number of hairs per unit area in a horizontal plane cutting through the bundle, and θ, the average angle that those hairs make with respect to the vertical. Each of these depends on the vertical coordinate z and the radial distance r from the centreline of the ponytail. The simplest approximation for ρ is that it is uniform at any given value of z, so the number of hairs n(r) within a radius r is just proportional to the area of a circle of radius r, and hence
where R(z) is the function that describes the outer edge of the ponytail and N is the total number of hairs.
In dealing with the angle θ we can see that a straight line corresponds to a constant value of θ whereas when the angle varies with position the average hair has some curvature κ. To describe that curvature we can imagine drawing an inscribed circle tangent to the curve at a given point, where the radius P of that circle defines the curvature as κ=1/P. As described first by the Swiss mathematicians Leonhard Euler and Jakob Bernoulli, elastic filaments have an energy per unit length that is the square of the local curvature in the form
where A is the bending modulus we discussed earlier. The lowest energy is a straight filament with κ=0 and bending the filament with either positive or negative curvature leads to an increase in energy. In applying this idea to the ponytail, we can see that the simplest picture is one in which the angle that the average hair orientation makes with respect to the vertical varies smoothly from zero at r=0 to the angle defined by the outer edge shape R(z), so
where the slope of the outer edge, dR/dz, is tan θ at that point, which is approximately θ for a shallow slope.
From this discussion we have the ingredients to describe the energy of a ponytail apart from the contributions from the meanderings of individual hairs away from the average orientation given by the angle θ. To make progress we realize that the interactions between neighbouring hairs will tend to compress those bends, and therefore will cost elastic energy. It is very hard to calculate this effect from first principles, so an alternative approach is to assume that this contribution depends only on the local density and to examine its consequences.
Ponytail Shape Equation
Overlaid images of hairs from a ponytail
The result of a straightforward calculation shows that the energy of the entire bundle of hair can be re-expressed in terms of the shape R(z) of the outer boundary alone as if it were a single fibre with slightly altered material properties. That equivalent fibre has elasticity, tension, and weight, and in addition is subjected to a radial force we call the bundle pressure arising from the random curliness of the hair. This pressure deflects the edge outward so as to swell the bundle from what it would otherwise be. We can see the relative importance of these contributions on the graph shown in the lecture, where it is clear that apart from the region just below the clamp at the top of the ponytail the balance of forces is between the pressure and the weight of hair.
Statistics of Random Curvatures, measurements on 115 hairs from a commercial* switch, using high-resolution stereographic imaging. Filament reconstruction based in part on an algorithm due to W.S. Ryu for C. elegans tracking.
Given this simplicity, we can analyse the shapes of real ponytails and from the form of the outer boundary deduce the as yet unknown pressure. As shown in the slides, this was done by examining multiple ponytails that were held on a rotatable support, allowing us to take images of each ponytail from five different angles and average them to arrive at a smooth average shape. Analysing the outer edge of the images we can extract the pressure as a function of the radius. Remarkably, it is a simple linear function of R, meaning that the bundle acts like a spring, with force proportional to displacement. This is known as Hooke’s law, and it can be understood by considering the energetics of confining a meandering fibre inside a cylinder formed by the other fibres.
“Observe the motion of the surface of the water which resembles that of hair, and has two motions, of which one goes on with the flow of the surface, the other forms the lines of the eddies…” – The Notebooks of Leonarda da Vinci
Finally, we can provide a further experimental test of this theory, the experimentum crucis, to borrow a phrase from Isaac Newton, by extracting from measurements on a full-length ponytail the physical parameters of a given type of hair and then comparing the theory’s prediction as we cut the hair shorter and shorter. As you can see from the slide, the theory works rather well indeed.
Swing of the Ponytail
In this last part of the lecture I want to turn to the motion of ponytails, and in particular the familiar “swing” of a ponytail experienced by a jogger as her head moves up and down and her ponytail bounces from side to side. As is often the case, ‘familiarity should not be confused with understanding’, and the explanation for this behaviour turns out to be rather subtle.
Ponytail motion
Our starting point for the discussion is a paper by the experimental physicist Michael Faraday, famous of course for his work on electromagnetism. In 1831 Faraday published a lengthy and detailed paper [2] on the patterns assumed by sand grains bouncing on a solid plate that is set in vibration, for example by a violin bow stroked along its edge. These so-called Chladni figures had been studied in the past, and Faraday’s primary goal in the paper was to explain in detail the regular geometric patterns. But in a famous appendix to the paper, he provides the first serious discussion of the analogous patterns found in a fluid when its container is oscillated. We have all seen the fascinating wavelike surface undulations that occur when we rub our fingers on a wine glass or slide a Styrofoam cup containing coffee across a surface. After a lengthy discussion of the circumstances leading to this behaviour, Faraday made a remarkable observation: that the patterns of periodic surface undulations repeat with a frequency that is exactly one-half that of the forcing applied to the fluid. This is very different from what we see in other contexts, such as when we push a child on a swing and the swing responds at the same frequency as our pushing, once per cycle. This behaviour is technically known as a “subharmonic” response. Modern experiments have continued to probe these dynamics [3].
The class of mathematical problems in which some parameter of a system is made to oscillate periodically in time is now associated with the name of the mathematician George William Hill who studied them in the context of celestial mechanics. He was interested in understanding the effects of other heavenly bodies on the motion of the moon, with the orbits of those bodies bringing them closer and further over time, periodically. He derived mathematical results to describe the relationship between the frequency of forcing and the frequency of response in these systems.
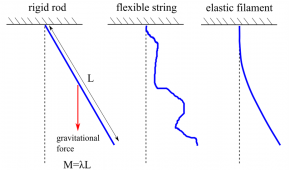
The great 20th century applied mathematician Joseph Keller, who passed away this summer at the age of 93, wrote a wonderful paper [4] on the swing of the ponytail in 2010, synthesizing the ideas of Faraday and Hill to explain the familiar feature that while the jogger’s head moves up and down her ponytail moves side to side. Keller considered that a ponytail might be modelled like a rigid rod acting like a pendulum, or perhaps better as a flexible string, and best as an elastic string that resists bending in much the same way we discussed earlier in our calculation of the shape of the ponytail. His essential result was obtained using the first model. Here, by oscillating the support up and down sinusoidally with some amplitude a and frequency ω we achieve an acceleration , so the gravitational acceleration is modified to , a parametric forcing of the system.
In the simple rigid-rod model of a ponytail, one can show that the natural frequency of oscillation is
Hill’s results for systems of this kind shows that when the ratio between the natural frequency and the driving frequency satisfies the relationship
for k=1,2,3,…, then the pendulum will be set in lateral motion. The lowest solution is k=1, for which we see the subharmonic relationship that Faraday described. Keller then used the typical length of a ponytail L=25 cm and deduced that a jogger taking about 140 or so steps per minute would excite the lateral motion. This is spot on.
To study this problem in detail we have begun a laboratory investigation of this problem using a precise motorised support, high-speed imaging, and image analysis to track a ponytail subjected to vertical oscillations. The results are shown in the movie, where the subharmonic character is clear.
Hair Tangling
Tangling: The next frontier
Finally, I would like to close with a brief example of where this research is headed next. As mentioned at the beginning, the original motivation for the research on ponytails was to understand the phenomenon of hair tangling. We have all experienced how, during the act of combing long hair, the comb may literally get stuck in a `knot’. This is not a knot in the literal sense, as the ends of the hair fibres are free, but it is some kind of jamming process which effectively stops the comb from moving. It appeared to us that the only way to understand this was to build an experiment in which we could watch what individual hairs are doing as the lock-up occurs. The experiment consists of a light table on which is a comb held within a Perspex clamp, and a motorised stage that moves a bundle of hairs past the comb. A high-resolution camera with a macro lens records the tangling in real time. The movie shows the complexity of this process.
References
[1] Shape of a Ponytail and the Statistical Physics of Hair Fiber Bundles, R.E. Goldstein, P.B. Warren, and R.C. Ball, Phys. Rev. Lett. 108, 078101 (2012)
[2] On a Peculiar Class of Acoustical Figures; and on Certain Forms Assumed by Groups of Particles upon Vibrating Elastic Surfaces, M. Faraday, Phil. Trans. R. Soc. Lond. 121, 299 (1831)
[3] Experimental study of the Faraday instability, S. Douady, J. Fluid Mech. 221, 383 (1990)
[4] Ponytail motion, J.B. Keller, SIAM J. Appl. Math. 70, 2667 (2010)