Portrait of Galileo by Justus Sustermans, 1636, oil on canvas / National Maritime Museum, London, Wikimedia Commons
By Dr. Albert Van Helden
Professor Emeritus of History
Rice University
Overview
Galileo Facing the Roman Inquisition, by Cristiano Banti, 1857, oil on canvas / University of Missouri, Creative Commons
Galileo’s Early Life
Galileo was born in Pisa, Italy on February 15, 1564. His father, Vincenzo Galilei, was a musician. Galileo’s mother was Giulia degli Ammannati. Galileo was the first of six (though some people believe seven) children. His family belonged to the nobility but was not rich. In the early 1570’s, he and his family moved to Florence.
The Pendelum
n 1581, Galileo began studying at the University of Pisa, where his father hoped he would study medicine. While at the University of Pisa, Galileo began his study of the pendulum while, according to legend, he watched a suspended lamp swing back and forth in the cathedral of Pisa. However, it was not until 1602 that Galileo made his most notable discovery about the pendulum – the period (the time in which a pendulum swings back and forth) does not depend on the arc of the swing (the isochronism). Eventually, this discovery would lead to Galileo’s further study of time intervals and the development of his idea for a pendulum clock.
On Motion
In 1581, Galileo began studying at the University of Pisa, where his father hoped he would study medicine. While at the University of Pisa, Galileo began his study of the pendulum while, according to legend, he watched a suspended lamp swing back and forth in the cathedral of Pisa. However, it was not until 1602 that Galileo made his most notable discovery about the pendulum – the period (the time in which a pendulum swings back and forth) does not depend on the arc of the swing (the isochronism). Eventually, this discovery would lead to Galileo’s further study of time intervals and the development of his idea for a pendulum clock.
Mechanical Devices
In 1592, Galileo was appointed professor of mathematics at the University of Padua. While teaching there, he frequently visited a place called the Arsenal, where Venetian ships were docked and loaded. Galileo had always been interested in mechanical devices. Naturally, during his visits to the Arsenal, he became fascinated by nautical technologies, such as the sector and shipbuilding. In 1593, he was presented with the problem involving the placement of oars in galleys. He treated the oar as a lever and correctly made the water the fulcrum. A year later, he patented a model for a pump. His pump was a device that raised water by using only one horse.
Family Life
Galileo was never married. However, he did have a brief relationship with Marina Gamba, a woman he met on one of his many trips to Venice. Marina lived in Galileo’s house in Padua where she bore him three children. His two daughters, Virginia and Livia, were both put in convents where they became, respectively, Sister Maria Celeste and Sister Arcangela. In 1610, Galileo moved from Padua to Florence where he took a position at the Court of the Medici family. He left his son, Vincenzio, with Marina Gamba in Padua. In 1613, Marina married Giovanni Bartoluzzi, and Vincenzio joined his father in Florence.
Telescope
Galileo invented many mechanical devices other than the pump, such as the hydrostatic balance. But perhaps his most famous invention was the telescope. Galileo made his first telescope in 1609, modeled after telescopes produced in other parts of Europe that could magnify objects three times. He created a telescope later that same year that could magnify objects twenty times. With this telescope, he was able to look at the moon, discover the four satellites of Jupiter, observe a supernova, verify the phases of Venus, and discover sunspots. His discoveries proved the Copernican system which states that the earth and other plaqnets revolve around the sun. Prior to the Copernican system, it was held that the universe was geocentric, meaning the sun revolved around the earth.
The Inquisition
Galileo’s belief in the Copernican System eventually got him into trouble with the Catholic Church. The Inquisition was a permanent institution in the Catholic Church charged with the eradication of heresies. A committee of consultants declared to the Inquisition that the Copernican proposition that the Sun is the center of the universe was a heresy. Because Galileo supported the Copernican system, he was warned by Cardinal Bellarmine, under order of Pope Paul V, that he should not discuss or defend Copernican theories. In 1624, Galileo was assured by Pope Urban VIII that he could write about Copernican theory as long as he treated it as a mathematical proposition. However, with the printing of Galileo’s book, Dialogue Concerning the Two Chief World Systems, Galileo was called to Rome in 1633 to face the Inquisition again. Galileo was found guilty of heresy for his Dialogue, and was sent to his home near Florence where he was to be under house arrest for the remainder of his life. In 1638, the Inquisition allowed Galileo to move to his home in Florence, so that he could be closer to his doctors. By that time he was totally blind. In 1642, Galileo died at his home outside Florence.
Introduction to Galileo Galilei
Portrait of Galileo, by Ottavio Leoni, stone drawing on paper / Biblioteca Marucelliana
Galileo was born in Pisa, Italy on February 15, 1564. His father, Vincenzo Galilei, was a musician. Galileo’s mother was Giulia degli Ammannati. Galileo was the first of six (though some people believe seven) children. His family belonged to the nobility but was not rich. In the early 1570’s, he and his family moved to Florence.
Galileo was never married. However, he did have a brief relationship with Marina Gamba, a woman he met on one of his many trips to Venice. Marina lived in Galileo’s house in Padua where she bore him three children. His two daughters, Virginia and Livia, were both put in convents where they became, respectively, Sister Maria Celeste and Sister Arcangela. In 1610, Galileo moved from Padua to Florence where he took a position at the Court of the Medici family. He left his son, Vincenzio, with Marina Gamba in Padua. In 1613, Marina married Giovanni Bartoluzzi, and Vincenzio joined his father in Florence.
Galileo’s Education
Collegio Romano
In 1534 Ignatius de Loyola and six companions bound themselves in vows of poverty, chastity, and apostolic labors. Six years later, Pope Paul III recognized the order as the Society of Jesus and authorized the framing of a detailed constitution. Rather than turning away from daily life in the tradition of monastic orders, the Jesuits formulated their mission in the world at large, and specifically in three areas, teaching, service to the nobility, and missionary work in foreign lands. In all three areas they were extraordinarily successful, but almost from the start they made their greatest mark in education. By 1556, when the Society had about a thousand members, three-fourths were engaged in education in 46 colleges. In 1579 there were 144 colleges, and by 1626 444 colleges, 56 seminaries, and 44 houses of training for Jesuits. At the apex of all Jesuit seminaries stood the Collegio Romano, founded by Ignatius in 1551. By papal bulls of 1552 and 1556 it received the right to grant doctorates in philosophy and theology as well as the privileges enjoyed by the universities of Paris, Louvain, Salamanca, and Alcalà. By 1567 the Collegio Romano had over a thousand students, and Pope Gregory XIII erected a large building to house the students and faculty. Over the years the college gradually became known as the Gregorian University in honor of that pope.
Although the mathematical sciences occupied a subservient role in the curriculum, they did have a role. In the ratio studiorum (curriculum rules) promulgated in 1566, we find the following:
Concerning mathematics, the mathematician shall teach, in this order, the [first] six books of Euclid, arithmetic, the sphere [of Sacrobosco], cosmography, astronomy, the theory of the planets, the Alphonsine Tables, optics, and timekeeping. Only the second year philosophy students shall hear his lecture, but sometimes, with permission, also the students of dialectics.
Over the next four decades, Christoph Clavius promoted the dignity of the mathematical (i.e. scientific) subjects and produced a series of textbooks that defined Jesuit scientific education not only in the Collegio Romano but in all Jesuit colleges. The influence of Jesuit mathematical education was felt in non-Jesuituniversities as well. It has been shown over the past two decades that Galileo’s lecture notes from his days as a student at the university of Pisa had as their ultimate source the lectures of the mathematicians at the Collegio Romano.
The Collegio Romano attracted the best scientists in the Society, and Jesuit educators as far away as China turned to them for their judgment on scientific matters. In 1610 there were four mathematicians on the faculty, Christoph Clavius, Christoph Grienberger, Paolo Lembo, and Odo van Maelcote. It is to these four men that other Jesuits and high church officials turned for a verdict on the new phenomena Galileo claimed to have discovered with his telescope.
Accademia dei Lincei
Portrait of Federico Angelo Cesi, by Pietro Fachetti, oil on canvas / Institute and Museum of the History of Science, Florence
The Cesi family belonged to the high aristocracy of Rome and the Papal States. It originated in the little town of Cesi, near Rome, and its wealth derived largely from high offices connected with the church. (Frederico Cesi’s paternal uncle, Bartolomeo Cesi, became a cardinal.) At the turn of the seventeenth century, its wealth was being eroded (like that of similar Roman families) by the ruinous expense of keeping up their “life-style of the rich and famous.” The many titles held by members of the family were mostly empty honors with little or no economic significance.
Cesi, son of Federico Cesi (hereditary Marquis of Monticello and Duke of Acquasparta, and later made a prince by Pope Paul V) and Olimpia Orsini, was born in Rome in 1585. He was educated privately and at an early age became interested in natural science. He was convinced, however, that nature should be studied directly, not through the filter of Aristotelian philosophy–an idea that was being enunciated by a growing number of learned men, among whom the most influential voice was to become that of Francis Bacon.
Cesi’s father was strongly opposed to the career direction in which these studies were taking young Federico, but his mother (herself from a wealthy and powerful Roman family, the Orsini) provided him with both moral and financial support.
Coat of Arms of the Accademia dei Lincei / Institute and Museum of the History of Science, Florence
In 1603, at age eighteen, Cesi founded the Accademia dei Lincei, the Lyncean Academy. Its name came from Lynceus, the argonaut of Greek mythology renowned for his sharpness of sight. Its initial members were Cesi, the mathematician Francesco Stelluti, the physician Johannes Eck from the Low Countries, and the polymath [a person of great learning in several fields of study] Anastasio De Fillis. The members lived communally and almost monastically in Cesi’s house, where he provided them with books and laboratory equipment. In a 1605 document, the goals of the academy were stated to be “not only to acquire knowledge of things and wisdom, and living together justly and piously, but also peacefully to display them to men, orally and in writing, without any harm.” Cesi devoted the rest of his life to these goals and his academy.
The Lyncean Academy was steadfastly opposed by Cesi’s father and other Roman aristocrats. Its members were accused of black magic, opposition to Church doctrine, and living a scandalous life. Eck was forced to leave Rome, and for some time the membership of the academy was scattered. Cesi kept in close contact with all of them through correspondence. During a stay in Naples, Cesi came to know the polymath Giambattista della Porta, and he considered setting up a branch of the academy in that city. Porta became a member of the academy in 1610.
The most famous member of the academy was Galileo, who was inducted in the spring of 1611, during his visit to Rome. The academy’s most celebrated publications were those of Galileo, first his Letters on Sunspots in 1613, and then his Assayer in 1623. After Galileo’s induction, the membership grew rapidly, and at its height the Lyncean Academy had 32 members, including many in foreign countries.
Cesi’s academy was very much a personal academy. Its impetus and funds came from him exclusively. When, in 1630, he died suddenly, his academy died with him. Galileo was just beginning the tedious process of obtaining a license for his Dialogue Concerning the Two Chief World Systems, and the plan had been for the academy to sponsor the book and pay for the printing costs.
Galileo’s Patrons
Duke of Mantua, Vincenzo Gonzaga (1562-1612)
Portrait of Vincenzo Gonzaga, by Peter Paul Rubens, 1500, oil on canvas / Villa Perdomini
The City of Mantua, located in the northern Italian plain (see map), had for centuries been a center of cloth manufacture. The wealth of the city made possible a brilliant court culture under the Gonzaga. This family had ruled the city since 1329, initially as “Captains General of the People,” and since 1530 as Dukes. Because of the city’s wealth and the Gonzaga support of arts and letters, the Mantua court became one of the most brilliant in Italy.
At the turn of the seventeenth century, Mantua was in economic decline. Although Vincenzo Gonzaga was still one of the great patrons in Italy, his spendthrift habits were accelerating the decline of the city, and after his death in 1612 Mantua ceased being an important cultural center.
Vincenzo Gonzaga had been tutored in the mathematical subjects by Giuseppe Moletti, Galileo’s predecessor in the chair of mathematics at the University of Padua. During the winter of 1603-1604, Galileo visited the Mantuan court in an effort to obtain a position there. He was offered a salary of 300 ducats per year plus living expenses for himself and a servant. At this time Galileo’s salary at the University of Padua was 320 ducats, and he had further income from his boarding students. He therefore requested instead a salary of 500 ducats with an expense account for himself and two servants. No terms could be worked out, and Galileo retained his post in Padua. But for one of his proportional compasses (no doubt an especially ornate one) and his instruction manual, the Duke did give Galileo a gold chain with a medal, and two silver dishes. It was the custom that the medal could not be sold but that the chain and the cups could. In his account books for 1604 Galileo put down the chain for 900 lire and the cups for 440 lire.
The Medici Family
Medici Coat of Arms / Wikimedia Commons
The Medici family of Florence can be traced back to the end of the 12th century. It was part of the patrician class [aristocracy, nobles], not the nobility, and through much of its history the family was seen as the friends of the common people. Through banking and commerce, the family acquired great wealth in the 13th century, and political influence came along with this wealth. At the end of that century, a member of the family served as gonfaliere, or standard bearer (high ceremonial office) of Florence. In the 14th century the family’s wealth and political influence increased until the gonfaliere Salvestro de’ Medici led the common people in the revolt of the ciompi (small artisanate). Although Salvestro became the de facto dictator of the city, his brutal regime led to his downfall and he was banished in 1382. The family’s fortune then fell until it was restored by Giovanni di Bicci de’ Medici (1360-1429), who made the Medici the wealthiest family in Italy, perhaps Europe. The family’s poltical influence again increased, and Giovanni was gonfaliere in 1421.
Giovanni’s son, Cosimo (1389-1464), Cosimo il Vecchio (the old or first Cosimo), is considered the real founder of the political fortunes of the family. In a political struggle with another powerful family, the Albizzi, Cosimo initially lost and was banished, but because of the support of the people he was soon recalled, in 1434, and the Albizzi were banished in turn. Although he himself occupied no office. Cosimo ruled the city as uncrowned king for the rest of his life. Under his rule Florence prospered.
Cosimo il Vecchio di Medici, from the Workshop of Bronzino, oil on tin / Uffizi Gallery
Cosimo spent a considerably part of his huge wealth on charitable acts, live simply, and cultivated literature and the arts. He amassed the largest library in Europe, brought in many Greek sources, including the works of Plato, from Constantinople, founded the Platonic Academy and patronized Marsilio Ficino, who later issued the first Latin edition of the collected works of Plato. The artists supported by Cosimo included Ghiberti, Brunelleschi, Donatello, Alberti, Fra Angelico, and Ucello. During his rule and that of his sons and grandson, Florence became the cultural center of Europe and the cradle of the new Humanism. Cosimo’s son Piero (1416-1469) ruled for just a few years but continued his father’s policies while enjoying the support of the populace.
Piero’s sons, Lorenzo (1449-1492) and Giuliano (1453-1478) ruled as tyrants, and in an attack in 1478 Giuliano was killed and Lorenzo wounded. If the family fortunes dwindled somewhat and Florence was not quite as prosperous as before, under Lorenzo, known as the Magnificent, the city surpassed even the cultural achievements of the earlier period. This was the high point of the Florentine Renaissance: Ficino, Giovanni Pico della Mirandola, Boticelli, Michelangelo, etc. But Lorenzo’s tyrranical style of governing and hedonistic lifestyle eroded the goodwill of the Florentine people. His son Piero (1472-1503) ruled for just two years. In 1494, after accepting humiliating peace conditions from the French (who had invaded Tuscany), he was driven out of the city and died in exile. For some time, Florence was now torn by strife and anarchy and, of course, the rule of Savanarola – a Dominican friar, prior of the convent of San Marco in Florence, Savonarola believed that he was sent as a watchman for God to warn people of impending doom. His power was such that when the Medici family was expelled in 1494, he ruled the city and became a major power in Italy. In 1496, he turned against the pope, after the pope attempted to control the prior’s power by offering a cardinal’s office. In 1497, the pope excommunicated Savonarola. Savonarola continued to practice as a priest, refuting the order. In the end, Savonarola was tortured and in 1498 was hanged.
Upon the defeat of the French armies in Italy by the Spanish, the Spanish forced Florence to invite the Medici back. Piero’s younger brother Giuliano (1479-1516) reigned from 1512 to 1516, and became a prince; he was followed by Lorenzo (1492-1519), son of Piero, who was named Duke of Urbino by Pope Leo X (himself a Medici, son of Lorenzo the Magnificent); and upon Lorenzo’s death, Giulio (1478-1534), the illigitimate son of Lorenzo the Magnificent’s brother Giuliano, became rule of the city but abdicated in 1523 in favor of his own illegitimate son, Alessandro (1510-1537), to become Pope Clement VII. Alessandro became hereditary Duke of Florence.
If the rulers since Lorenzo the Magnificent had been weak and ineffective, this changed when Cosimo I (1519-1574) ascended the throne in 1537 at the age of 18. Cosimo was a descendant not of Cosimo il Vecchio but from Cosimo’s brother. He quickly consolidated his power, and under his rule Tuscany was transformed into an absolutist nation state. Although politically ruthless, Cosimo was highly cultured and promoted letters and arts as well as the Tuscan economy and navy. He founded the Accademia della Crusca, a body charged with the promotion of the Tuscan language (which has become the standard Italian of today), the Accademia del Disegno (Academy of Design), renewed the university of Pisa, and conquered Siena and Lucca.
Cosimo I di Medici / Institute and Museum of the History of Science, Florence
In 1569 Cosimo was named Grand Duke of Tuscany. He set the style for the new absolute rule by concentrating the administration of Florence in a new office building, the Uffizi (where he also began a small museum for art works; the entire Uffizi is now a museum), and moving his residence across the river to the Pitti Palace, bought in 1549 and enlarged and remodeled several times by Cosimo and his descendants. He built a private corridor between the Pitti Palace and the Palazzo Vecchio in the city, where the government met. Vincenzo Galilei moved his family, including the ten-year old Galileo, from Pisa to Florence in the year of Cosimo’s death.
Cosimo’s son, Francesco I (1541-1587) was an ineffectual ruler under whom Tuscany languished. His younger brother, Ferdinand (1549-1609), who had been made a cardinal at the age of fifteen, became Grand Duke upon Francesco’s death in 1587. Ferdinand II was a capable administrator under whom Tuscany flourished again.
Ferdinand was an admirer of Tomasso Campanella and tried to protect him as best he could. He was interested in scientific matters, and had a great armillary sphere [an instrument consisting of an arrangement of rings, all of which are circles of the same sphere, used to show the relative positions of the celestial equator, ecliptic, and other circles of the clestial sphere] constructed by Antonio Santucci, his cosmographer.
Left: Holy Roman Emperor Ferdinand I, by Hans Bocksberger the Elder, c.1550, oil on paper mounted on wood / Kunsthistorisches Museum
Right: Antonio Santucci’s Armillary Sphere / Hall III in Museo Galileo
Ferdinand appointed Galileo to the professorship of mathematics at the university of Pisa in 1588. In the year of his accession, Ferdinand married Christina of Lorraine (1565-1637), who was the grand daughter of Catherine de’ Medici, Queen of France. Christina was well-disposed to Galileo and as a favor in return for some services rendered by Galileo when he was still in Padua found a position for his brother in law Benedetto Landucci. It was to Christina that Galileo later wrote his letter on science and scripture, “Letter to the Grand Duchess Christina of Lorraine.”
Ferdinand and Christina had four sons and four daughters. The eldest son, Cosimo II, ascended the throne upon his father’s death in 1609. Galileo had tutored Cosimo in mathematics during some summers, and therefore the young Grand Duke knew him well and admired him enough to offer him a court position in 1610, after Galileo had dedicated Sidereus Nuncius to him and his family. After a bout of fever, in 1615, Cosimo’s health deteriorated, and he died in 1620.
Left: Portrait of Christine of Lorraine, by Scipione Pulzone, c.1595, oil on canvas / Uffizi Gallery
Right: Portrait of Cosimo II di Medici, Großherzog von Toskana, by Justus Sustermans, 17th century, oil on canvas / Uffizi Gallery
Cosimo’s son, Ferdinand II (1610-1670) was just ten years old when he became Grand Duke, and until his majority the government was carried on by the two Grand Duchesses, Cosimo’s mother Christina of Lorraine, and Cosimo’s wife, Maria Magdalena of Austria, the sister of the Holy Roman Emperor Ferdinand II.
Holy Roman Emperor Ferdinand II, c.1614, oil on canvas / Kunsthistorisches Museum
During the outbreak of the plague, in 1630, Ferdinand distinguished himself, but he was not a strong ruler and was unable to protect Galileo from the Inquisition in 1633. In 1657, together with his brother Leopold, Ferdinand established the Accademia del Cimento, or Academy of Experiment, a forerunner of more permanent scientific academies, such as the Royal Society of London (1665) and the Royal French Academy of Sciences (1666). The Accademia del Cimento stopped functioning in 1667.
The Florentine and Tuscan economy had been slowly stagnating since the end of the sixteenth century. Under Ferdinand II, his son, Cosimo III (1642-1723), and his grandson, Gian-Gastone (1671-1737), the city country slipped into insignificance. Cosimo III’s rule was one of incompetence and religious intolerance. Gian-Gastone’s rule was too short to repair the damage. In 1735, an arrangement was made between Austria, France, England, and the Netherlands that a swap should be made with Lorraine going to France and Tuscany to Austria in return. In 1737 Austrian troops occupied Tuscany. One of Gian Gastone’s last acts was to erect a memorial to Galileo in the church of Santa Croce and to inter Galileo remains there. During the transference, several parts of Galileo’s skeleton were taken as relics by various people. One of Galileo’s fingers is now housed in the Museum of History of Science in Florence.
Gian-Gastone had no male heir, and the House of Medici died with him.
Maria di Medici, Queen of France, by Scipione Pulzone or Frans Pourbus the Younger, 17th century, oil on canvas / Galleria Palatina
The Medici family dominated Florentine politics for two and a half centuries and presided over a cultural achievement that is equalled only by Athens in the golden age. The family also got its genes mixed with those of most royal families in Europe. Medici women included Catherine (1519-1589) who married Henry II, King of France and ruled the coutry after her husband’s death; Maria (1573-1642) married Henry IV, King of France. Maria’s daughters became queens of Spain and England. Cosimo II’s wife, Maria Magdalena, was the sister of Ferdinand II, Holy Roman Emperor.
Paolo Sarpi
Paolo Sarpi, by George Vertue, engraving / Wikimedia Commons
Pietro (his birth name) Sarpi was born in Venice, the son of Francesco Sarpi, a struggling merchant from San Vito (northwest of the city), and Isabella Morelli a Venetian from a good family. Francesco died young, and young Pietro was educated by his mother’s brother, a priest and school master, and then by Fra Giammaria Capella, a monk in the Servite Order. In 1566, at the age of fourteen, Pietro was received in the Servite Order and took the name of Paolo. By the time he was ordained a priest, in 1574, Sarpi was an immensely learned monk, trained in philosophy, theology, mathematics, Greek, and Hebrew. His first assignment was as an assistant to Cardinal Carlo Borromeo in Milan. He was recalled to Venice a few years later and rose rapidly in the Servite Order. In 1579 he became Provincial of Venice [the head of an ecclesiastical province, or a member of a religious order presiding over the order in a given district or province] and was chosen as one of three Servite scholars to revise the constitution and rule of the Order. In connection with this task, Sarpi spent some time in Rome to study the decrees of the Council of Trent. Here he became friends with Robert Bellarmine, although later they became opponents. Back in Venice, Sarpi became Procurator General1 of the Venetian province of the Order in 1584 and served as Vicar-General from 1599 to 1604. He lived in quiet retirement in his monastery, performing his religious tasks and pursuing his private studies.
Paoli Sarpi, by Jacobus Houbraken, 1721 / Peace Palace Library, The Hague, Netherlands
Beginning in the 1590s, disputes between Rome and the Venetian Republic over jurisdictional issues became frequent. As a result Paul Paul V put the Republic under interdict in 1606, forbidding the clergy to perform their usual offices. Venice ordered the clergy to disobey the papacy and expelled the orders that did not do so, including the Jesuits. Sarpi, who was a patriot, sided with the Republic against the Pope and became Venice’s official theologian in that year. He refused to obey a summons to come to Rome and in 1607 was wounded by assassins widely thought to be sent by the Pope. Sarpi published a number of books on jurisdictional issues (including the first history of the Council of Trent), taking a strictly historical approach. He carried on a wide correspondence with scholars and diplomats, including heretics. Although it has been claimed that he had sympathies for Protestants, it is perhaps more appropriate to say that he was against religious excesses and the secular powers claimed by the Pope.
Sarpi was a friend and benefactor of Galileo. He first acquainted his friend with the reports from the Netherlands about devices for seeing faraway (telescopes) and facilitated Galileo’s offer of an eight-powered spyglass to the Venetian government (and the reward) in 1609. Galileo and Sarpi discussed and corresponded about various other subjects, including magnets, the tides, and the law of falling bodies.
Pope Urban VIII
Pope Urban VIII (Maffeo Barberini), by Pietra da Cortona, 1627, oil on canvas / Capitoline Museums
The Barberini were a powerful family, with branches in Rome and Florence, which had produced several cardinals up to that point. Maffeo was born into the Florentine branch of the family in 1568. His father died when Maffeo was only three years old; his mother insisted that he be educated by the Jesuits–first in Florence, and later in Rome at the Jesuit Collegio Romano. Here he lived with his uncle, Francesco Barberini, who held the high church office of Protonotary Apostolic [a member of the first college of prelates of the Roman Curia. Charged chiefly with the registry of pontifical acts and canonizations. Also an honorary title for certain other prelates]. In 1589 he took the degree of doctor of law from the University of Pisa.
Maffeo Barberini’ s rise in the church hierarchy was rapid. In 1601 he served as papal legate [an ecclesiastic delegated by the pope as his representative] to the court of Henri IV, king of France; in 1604 he became archbishop [a bishop of the highest rank who presides over an archbishopric or archdioscese] of Nazareth (an office he obviously fulfilled in absentia since the Holy Land was under Moslem rule) and took up the post of papal nuncio (lit. messenger, the papal legate permanently accredited to a civil government) to the French king; in 1606 he was made a cardinal with the titular church of St. Peter in Montorio and later St. Onofrio; in 1608 he became bishop [priest who acts as the highest religious official in a diosces. One of the principal functions of the bishop was to celebrate the Eucharist] of Spoleto. As bishop, Barberini convened a synod, completed the construction of one seminary and built two others, and served as legate of Bologna and prefect [a cardinal in charge of a congregation in the Curia Romana] of the Segnatura di Giustizia. Upon the death of Pope Gregory XV, in1623, Maffeo Barberini was elected Pope, taking the name of Urban VIII. A synod is an assembly of ecclesiastics or other church delegates, convoked pursuant to the law of the church, for the discussion and decision of ecclesiastical affairs. A council within the Church. Diocesan councils consisted of the presbyters of a dioscese meeting under the presidency of the bishop. Provincial councils consisted of all the diosces in an ecclesiastical province, with the provincial in the role of the pre sident over the bishops of the province. Plenary councils were councils of several provinces. Patriarchal councils were of the provinces united in one patriarchate. The provinces in a country could form a national council. General councils could be of the East or West, or of the whole Church. Finally, Ecumenical Councils were those whose decisions were accepted by the Church as a whole.
During his long papacy, Urban VIII promoted missionary work. He formed dioceses [an area of land defined by the fact that all of the priests are responsible to a single bishop] and vicariats [office or authority of a vicar] in various missionary terrritories and founded a college for the training of missionaries. He also repealed the monopoly on missionary work in China and Japan given to the Jesuits [popular name for the monastic order called the Society of Jesus. The order was founded by Ignatius de Loyola in 1534, and was recognized by the pope in 1540. The mission of the Jesuits was in three areas: teaching, service to the nobility, and missionary work in foreign lands. Their greatest mark was made in education, and the Collegio Romano was their primary seminary] in 1585, opening these countries to missionaries of all orders. In 1639 he prohibited slavery among the Indians of Brazil, Paraguay, and the West Indies.
During this period the temporal power of the papacy was in greatest danger from the Hapsburg dynasty which ruled much of the German speaking region of Europe, the Southern Netherlands, and Spain. Spanish influence in Italy has been on the rise for a century, and the kingdom of Naples and Sicily, under Spanish rule, lay immediately to the South of the Papal State. For this reason, Urban VIII favored the anti-Hapsburg policy of the French, neglecting to support the catholic cause in Germany.
Urban VIII saw to it that the Barberini family benefited from his papacy. His brother and two nephews were made cardinals [high ecclesiastics appointed by the pope to the College of Cardinals and ranking above every other ecclesiastic but the pope] and given high church offices. Other family members were helped by the Pope in the acquisition of property and titles . He even went so far as to make war on Parma, Tuscany, Modena, and Venice over a matter of protocol involving his nephew-cardinals. Pope Urban strenghtened fortifications and armaments in the papal territories. He lavishly supported artists, chief among whom was Giovanni Lorenzo Bernini, who beautified St. Peter’s cathedral. Urban had the bronze supporting girders of the Roman Pantheon melted down and made into cannon and and other objects. This prompted the epigram: ” What the barbarians did not do the Barberini’s did.”
Maffeo Barberini was an accomplished man of letters, who published several volumes of verse. Upon Galileo’ s return to Florence, in 1610, Barberini came to admire Galileo’ s intelligence and sharp wit. During a court dinner, in 1611, at which Galileo defended his view on floating bodies, Barberini supported Galileo against Cardinal Gonzaga. From this point, their patron-client relationship flourished until it was undone in 1633. Upon Barberini’ s ascendance of the papal throne, in 1623, Galileo came to Rome and had six interviews with the new Pope. It was at these meetings that Galileo was given permission to write about the Copernican theory, as long as he treated it as a hypothesis. After the publication of Galileo’ s Dialogue Concerning the Two Chief Systems of the World, in 1632, the patronage relationship was broken. It appears that the Pope never forgave Galileo for putting the argument of God’s omnipotence (the argument he himelf had put to Galileo in 1623) in the mouth of Simplicio, the staunch Aristotelian whose arguments had been systematically destroyed in the previous 400-odd pages. At any rate, the Pope resisted all efforts to have Galileo pardoned.
Important Places
Florence and Tuscany
Aerial view of Florence / Wikimedia Commons
Tuscany is located in the western part of the boot of Italy, north of Rome and south of Genoa. It is bounded by the Apennines to the North and East and by the Mediterranean on the West. Its land area is about 9,000 square miles. Its major cities are Florence, Pisa, Siena, Lucca, Arezzo, and Pistoia. Its major river is the Arno, on which Florence and Pisa are located.
It was the home land of the Etruscans, which was annexed by Rome in 351 BC. After the fall of the Roman empire, the region, which became known as Tuscany (Toscana in Italian) came under the rule of a succession of rulers (Herulians, Ostrogoths, etc.) and emerged as a political entity with its own rulers. By the twelfth century the Tuscan cities were gradually gaining their independence as republics and forcing the nobility to live in the cities. By the high Middle Ages the cities of Pisa, Siena, Arezzo, Pistoia, Lucca, and especially Florence had become wealthy because of textile manufacture, trade, banking, and agriculture. Gradually Florence came to overshadow and conquer all other cities in the region.
After several experiments with representative government, Florence was ruled by an oligarchy of wealthy aristocrats, among whom the Medici family became dominant in the fifteenth century. Under the patronage of these wealthy families the arts and literature flourished as nowhere else in Europe. Florence was the city of such writers as Dante, Petrarch, and Macchiavelli, and artists and engineers such as Boticelli, Brunelleschi (who built the magnificent dome on the church of St. Mary of the Flowers), Alberti, Leonardo Da Vinci, and Michelangelo. Because of its dominance in literature, the Florentine language became the literary language of the Italian region and is the language of Italy today. Lorenzo de’ Medici, who ruled Florence in the late fifteenth century was perhaps the greatest patron of the arts in the history of the West.
But times changed. After Lorenzo the friar Savonarola ruled Florence, and the Medici were exiled. With the shift of commerce away from the Mediterranean and toward the Atlantic, after 1492, the economy of Tuscany went into a slow decline. In 1530 the Holy Roman Emperor Charles V conquered Florence and reestablished the Medici family in power. They were now dukes of Florence, and within a few decades Cosimo de Medici was made Grand Duke of Tuscany. Cosimo aggressively pursued a policy of economic revival, building the great harbor at Livorno because the harbor of Pisa had silted up.
Galileo was born under the rule of Cosimo in 1564. It was during this period that the Medici court increasingly firmly established its hold over the city. The court came to dominate all aspects of civic life, and for the Galilei family the route to success lay through the patronage structure in which the Court was central. In the seventeenth century Florence and Tuscany increasingly faded into obscurity and did not revive until the nineteenth century. It is today a major cultural center and attracts millions of tourists each year.
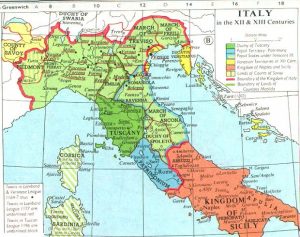
Italy
Map of medieval Italy / Wikimedia Commons
After the fall of the Roman Empire, the peninsula of Italy was not again politically unified until the nineteenth century. The region emerged from the so-called Dark Ages as an unorganized group of city states. Historically the most important of these were Venice (wealthy because of its trade with the Middle East) and Milan (an important manufacturing center) in the North, Florence (a center of commerce and manufacturing) and the Papal States in the center, and Naples and Sicily in the South. There were also many smaller and less important city states, such as Mantua, Genoa, and Verona.
During the high Middle Ages, ca. 1000-1450, the Italian region was economically and culturally the most advanced in Europe. Its wealth was based on trade with the Near East bringing spices, silk, and other desired Eastern commodities into Europe; manufacture, especially of finished cloth (Florence) and armaments (Milan), and banking. Italy’s wealth attracted the attention of foreigners, and for several centuries there was a contest between the papacy and the Holy Roman (German) Empire to control the region, but neither side succeeded.
It is in the city states, Florence chief among them, that Italian art, architecture, letters, and engineering flourished as never before, but in the long run these states were too small to be viable in a world increasingly dominated by the new, larger, nations states.
As the city states emerged independent from both Pope and Emperor, at the end of the Middle Ages, their never ending wars and intrigues against each other opened the door to other foreign intervention. Italy now became the victim of the ambitions of the new nation states of France and Spain. Sicily and Naples came under the rule of Spain and remained there until the nineteenth century, while Milan and Florence fell under the influence of France. Perhaps the most symbolic event was the sack of Rome by the troops of the Emperor, Charles V, in 1527. Moreover, with the voyages of Columbus and Vasco da Gama (partially financed by Italian capital) the economic center of Europe shifted away from the Mediterranean to the Atlantic coast. The new economic powers were, first, Portugal and Spain, and then France, the Netherlands, and England. Beginning in the sixteenth century, then, Italy began to slip with respect to Northern Europe, and by the end of the seventeenth century it had become a region of secondary economic and cultural importance.
During the Middle Ages the papal monarchy had claimed to be a supraregal political power (a claim the Popes did not give up until recently): the Pope claimed political primacy over counts, dukes, kings, and even the emperor. This struggle ended disastrously when the papacy was captured by the French king and moved to Avignon, where it remained from 1302 to 1378. From that date until 1417 there were, in fact, two popes, one in Rome and one in Avignon, and for a brief period, 1409-1415, there were three! With a single pope now again established in Rome, the papacy entered a period of unparalleled venality. The Renaissance popes were, it seemed at times, more interested in their pet projects in art and architecture or the careers of their relatives than in the well being of the Catholic Church. Reform was slow in coming. The occasion of the start of the Protestant Reformation, in 1517, was the selling of indulgences to raise money for the building of the cathedral of St. Peter in Rome.
There was, in Italy, a crisis of confidence in the sixteenth century. Many sought law, order, and security; republics fell, princes became more powerful; authority and titles were stressed (even if the latter had to be made up). The papal court became more Italian, and the Popes themselves gathered more and more power onto themselves, taking it away from the cardinals and bishops. At the same time the Church girded its loins for the battle against the Protestants. In 1540 Ignatius of Loyola founded the Society of Jesus, an order which owed obedience to the Pope; intermittently, from 1545 to 1563, the Council of Trent met and made a number of important pronouncements on the issues that separated the Protestants from the Catholic church. By the end of the sixteenth century the church was regaining territories that it had lost to Protestants.
The intellectual climate at this time was rather more restricted than it had been in earlier centuries. Orthodoxy was enforced; heterodoxies were combated. Giordano Bruno, an apostate monk who espoused the Copernican system and the infinitude of worlds (and inhabitants) was burned at the stake in 1600. It was in this climate that Galileo argued for the Copernican theory.
Galileo’s Family
Vincenzo Galilei
Della musica antica et della moderna, published in 1581 by Galileo’s father / Fiorenza
Vincenzo Galilei was born in Florence. He made his living as a lutenist, composer, theorist, singer, and teacher. Around 1560 he settled in Pisa, where Galileo Galilei was born in 1564, the oldest of six or seven children. During this period Galilei also studied for some time in Venice under the theorist Gioseffo Zarlino, with whom he later had a dispute about music theory. In the early 1570s Galilei and his family settled in Florence. His prowess as a musician and theorist attracted a number of powerful patrons, and he often spent time at their residences. e.g., in 1578-79 with Duke Albrecht of Bavaria in Munich.
Vincenzo Galilei published a number of books of musical scores for the lute and several books on musical theory. What is important about Galilei for our purposes is that he combined the practice and theory of music. Since antiquity, the theory of music had consisted of a mathematical discussion of harmony, in other words what are the mathematical ratios of the lengths of strings producing consonances, and how does one divide the octave? It had always been thought that not only was the ratio of lengths of two strings sounding an octave 2:1, but that so also was the ratio of the tensions of strings of equal lengths tuned an octave apart. Galilei showed that this is not the case: the ratio of tensions is 4:1. He found that ratio by hanging weights from strings. Here was an experiment that produced numbers and bore directly on the age-old theoretical discussions.
Stillman Drake argued that Galilei performed these experiments in 1588, when his son Galileo was living at home and giving private lessons in mathematics. The implication here is that young Galileo actually helped in the experiments. Be that as it may, Galileo received from his Florentine environment in general and from his father in particular the tendency to combine practical considerations with theory and to try to answer theoretical questions by experiment.
Maria Celeste
Suor Maria Celeste, daughter of Galileo, 17th century, oil on canvas / Wellcome Library Collection
Virginia, Galileo’s oldest child, was born in Padua on 12 August 1600. Her mother, Marina Gamba, was Galileo’s housekeeper. When Galileo moved to Florence, in 1610, he took Virginia and his other daughter, Livia (1601-1659), with him, leaving his son Vincenzio (only four years old) with his mother for a few years.
After he had settled in Florence, Galileo decided to put his two daughters in a convent for life. It took several years to make the arrangements. Not the least problem was that the girls were too young to make this important decision for themselves. Through the offices of Cardinal Maffeo Barberini, one of his admirers, Galileo obtained dispensation on this score, and in 1613 both girls were placed in the convent of San Matteo in nearby Arcetri, where the abbess was the sister of the secretary of the grand duke of Tuscany. Virginia took the veil in 1616, choosing the name of Sister Maria Celeste, and Livia followed the same course a year later, becoming Sister Arcangela.
Little is known about the life of Sister Maria Celeste until 1623, but about 120 letters to her father, written from 1623 to 1634 have survived. From these the picture of a loving daughter, always solicitous of her father’s well being, emerges. Her letter to her father of 21 November 1623 is typical:
Most Illustrious Lord Father,
I cannot rest any longer without news, both for the infinite love I bear you, and also for fear lest the sudden cold, which in general disagrees so much with you, should have caused a return of your usual pains and other complaints. I therefore send the man who takes this letter purposely to hear how you are, and also when you expect to set out on your journey I have been extremely busy at the dinner-napkins. They are nearly finished, but now I come to putting on the fringe, I find that of the sort of which I send you a sample, a piece is wanting for two dinner-napkins: that will be four braccia. I would be glad if you could let me have it immediately, so that I may send you the napkins before you go; as it was for this that I have been making such haste to get them finished.
As I have no cell of my own to sleep in, Sister Diamanta kindly allows me to share hers, depriving herself of the company of her own sister for my sake. But the room is so bitterly cold that with my head so infected, I do not know how I shall remain well, unless you can help me by lending me a set of those white bed-hangings which you will not want now. I would be glad to know if you can do me this service. Moreover, I beg you to be so kind as to send me that book of yours which has just been published, so that I may read it, for I have a great desire to see it.
These few cakes I send are some I made a few days ago, intending to give them to you when you came to bid us adieu. As you departure is not so near as we feared, I send them lest they should get dry. Sister Arcangela is still under medical treatment, and is much tried by the remedies. I am not well myself, but being so accustomed to ill health, I do not make much of it, seeing, too, that it is the Lord’s will to send me continually some such little trial as this. I thank Him for everything, and pray that He will give you the highest and best felicity. And finally, with all my heart, I greet you in the name of me and Sister Arcangela.
From San Matteo, the 21st of November 1623
Your most affectionate daughter Sister Maria Celeste Galilei
If you have collars to whiten, you can send them.
The convent of San Matteo was very poor. The nuns did not have the wherewithal to feed themselves and keep the buildings in repair. Maria Celeste wrote to her father that the bread was bad, the wine sour and that they ate ox meat. Galileo helped repair windows and personally took charge of keeping the convent clock in good repair. Maria Celeste often had to appeal to her father for help, and she was chronically ill. She bore her ill health with dignity and courage, and managed to be a great comfort to her father. She worked constantly to mitigate the difficulties between Galileo and her brother Vincenzio.
Villa Il Gioiello (the last home of Galileo Galilei) and Galileo’s hand-drawn plan, Florence / Wikimedia Commons
In 1631 Galileo bought the villa “Il Goiello” in Arcetri, near the convent. From this house he could see San Matteo and hear its bells. It was here that he spent his final years under house arrest. Part of the sentence that Galileo received in 1633 read as follows: “As a salutary penance we impose on you to recite the seven penitential Psalms once a week for the next three years.” Sister Maria Celeste took it upon herself to perform this penance for him. She died, however, on 2 April 1634, less than four months after Galileo’s return to Arcetri.
Marina Gamba
During one of his frequent trips to Venice, Galileo met a young woman named Marina di Andrea Gamba, with whom he entered into a relationship. Marina Gamba moved into Galileo’s house in Padua and bore him three children, Virginia (1600), later Sister Maria Celeste, Livia (1601), later Sister Arcangela, and Vincenzio (1606). In none of the three baptismal records is Galileo named as the father. In the case of Virginia, she was described as “daughter by fornication of Marina of Venice,” with no mention of the father; on Livia’s baptismal record the name of the father was left blank; and on Vinzenzio’s baptismal record “father uncertain.”The domestic situation was, apparently, a happy one, except when Galileo’s mother, Giulia, visited.
When Galileo left Padua for good to take up his position at the Medici court in Florence, in 1610, he took the two daughters with him but left Marina Gamba behind with Vincenzio, who was then only four years old. Vincenzio joined Galileo in Florence a few years later. In 1613 Marina Gamba married Giovanni Bartoluzzi. It appears that Galileo kept cordial relations with Gamba and Bartoluzzi.
Galileo put his two daughters in a convent. He managed to have Vincenzio legitimated by the Grand Duke of Tuscany. The reason for this unequal treatment is probably that Galileo would not be able to provide sufficiently large doweries for his daughters to allow them to make marriages appropriate to his stature at the Medici court. He would have no such financial obligation to his son.
Science
Instruments
The Pump
Model of Galileo’s pump / Institute and Museum of the History of Science, Florence
Galileo was appointed professor of mathematics at the University of Padua in 1592. The city of Padua had come under Venetian rule some time earlier, and the authorities in Venice regulated the university. Galileo quickly made friends among the Venetian patriciate and became a frequent visitor to the famous Arsenal, the inner harbor where Venetian ships were fitted out. Hulls of galleys entered on one end and within a few hours left at the other end, fully equipped and manned. The Arsenal had been a place of practical invention and innovation for centuries. Galileo had always been interested in mechanical things, and at the Arsenal he learned a great deal more about what we call technology, especially shipbuilding (His private lecture notes and other writings of this period are concerned with problems in fortification, mechanical devices, the sector, and other aspects of technology.) In 1593 he was consulted on the placement of oars in galleys and submitted a report in which he treated the oar as a lever and correctly made the water the fulcrum. A year later the Venetian Senate awarded him a patent for a device for raising water by means of one horse. The patent reads as follows:
That by the authority of this Council is granted to Mr. Galileo Galilei that for the space of the next twenty years others than him or his agents are not allowed in the city or any place in our state to make, have made, or, if made elsewhere, to use the device invented by him for raising water and irrigating fields, by which with the motion of only one horse twenty buckets of water that are contained in it run out continuously; under pains of losing the devices which will go to the supplicant, and 300 ducats, a third of which will be for the accuser, a third for the magistrate who undertakes the prosecution, and a third for our Arsenal; the supplicant being obligated, however, to have made known this new type of device within one year, and that it has not been invented or recorded by others, and that a patent has not been granted [on the same device] to others; otherwise the present grant will be void.
There is speculation that Galileo’s invention was an improvement of the Archimedean Screw (consisting of a core with a helical blade enclosed tightly in a casing), which was first used in Antiquity and patented in the Venetian Republic in 1567. I have found no evidence to support this speculation. Galileo apparently submitted a model of the device to the Venetian Senate, but this model has not survived. In the History of Science Museum in Florence, there is a model of a pump attributed to Galileo. This model dates from the second half of the eighteenth century (that is, more than a century after Galileo’s death), and which shows four pumps–not Archimedean Screws–driven by two horses which rotate an excentric device (see fig.). It appears to bear little relation to the device Galileo patented in 1594.
Although as time went on Galileo’s works became more and more “philosophical,” he never lost his interest in mechanical devices and technology in general. Although he was not the only “scientist” to have such interests, he was one of a handful in Europe who could bring their practical skills and insights to bear on science, as is shown by his experimental investigations of motion and strength of materials and by his development of, and discoveries with, the telescope.
Hydrostatic Balance
Model of Galileo’s hydrostatic balance / Wikimedia Commons
The “Eureka” story about Archimedes and the bath tub was as well known in Galileo’s day as it is in ours. Galileo, who was a great admirer of Archimedes and adopted many of his methods, probably read it in one of the editions of Vitruvius’s The Ten Books on Architecture, which was very popular in Renaissance Europe. Supposedly, it was in the bath tub that Archimedes figured out the solution to the problem posed to him by the king of Syracuse: was a crown (or wreath) supposedly made of pure gold in fact entirely gold? He measured the amount of water displaced by the crown and by an equal weight of gold, and found that the crown displaced more water. Its specific gravity [ratio of the density of any substance to the density of some other substance taken as standard, with water being the standard for solids] was thus less than that of gold, and therefore it had been adulterated with another metal.
Weighing precious metals in air and then in water was presumably a practice that was common among jewelers in Europe. Galileo had some ideas for refining the practice and, at the age of 22, he wrote a little tract about it, which he entitled La Bilancetta, or “The Little Balance.” What Galileo described was an accurate balance for weighing things in air and water, in which the part of the arm on which the counter weight was hung was wrapped with metal wire. The amount by which the counterweight had to be moved when weighing in water could then be determined very accurately by counting the number of turns of the wire, and the proportion of, say, gold to silver in the object could be read off directly.
This little tract illustrates the mixture of the theoretical and practical that marks Galileo’s science in contrast to that of most of his contemporaries.
Pendulum
Galileo’s pendulum clock / Institute and Museum of the History of Science, Florence
In Aristotelian physics, which was still the predominant way to explain the behavior of bodies near the Earth, a heavy body (that is, one in which the element earth predominated) sought its natural place, the center of the universe. The back and forth motion of a heavy body suspended from a rope was therefore not a phenomenon that could explain or illustrate much. It was outside the paradigm.
Galileo was taught Aristotelian physics at the university of Pisa. But he quickly began questioning this approach. Where Aristotle had taken a qualitative and verbal approach, Galileo developed a quantitative and mathematical approach. Where the Aristotelians argued that heavier bodies fell faster than lighter ones in the same medium, Galileo, early in his career, came to believe that the difference in speed depended on the densities of the bodies. Where Aristotelians maintained that in the absence of the resisting force of a medium a body would travel infinitely fast and that a vacuum was therefore impossible, Galileo eventually came to believe that in a vacuum all bodies would fall with the same speed, and that this speed was proportional to the time of fall.
Because of his mathematical approach to motion, Galileo was intrigued by the back and forth motion of a suspended weight. His earliest considerations of this phenomenon must be dated to his days before he accepted a teaching position at the university of Pisa. His first biographer, Vincenzo Viviani, states that he began his study of pendulums after he watched a suspended lamp swing back and forth in the cathedral of Pisa when he was still a student there. Galileo’s first notes on the subject date from 1588, but he did not begin serious investigations until 1602.
Galileo’s discovery was that the period of swing of a pendulum is independent of its amplitude–the arc of the swing–the isochronism [equal or uniform in time] of the pendulum. Now this discovery had important implications for the measurement of time intervals. In 1602 he explained the isochronism of long pendulums in a letter to a friend, and a year later another friend, Santorio Santorio, a physician in Venice, began using a short pendulum, which he called “pulsilogium,” to measure the pulse of his patients. The study of the pendulum, the first harmonic oscillator [each oscillation has a frequency that is an integer multiple of the same basic frequency], date from this period.
Galileo’s harmonic oscillator / Institute and Museum of the History of Science, Florence
The motion of the pendulum bob posed interesting problems. What was the fastest motion from a higher to a lower point, along a circular arc like a pendulum bob or along a straight line like on an inclined plane? Does the weight of the bob have an effect on the period? What is the relationship between the length and the period? Throughout his experimental work, the pendulum was never very far from Galileo’s thought. But there was also the question of its practical use.
A pendulum could be used for timing pulses or acting as a metronome for students of music: its swings measured out equal time intervals. Could the device also be used to improve clocks? The mechanical clock, using a heavy weight to provide the motive power, began displacing the much older water clock in the High Middle Ages. By incremental improvement, the device had become smaller and more reliable. But the accuracy of the best clocks was still so low that they were, for instance, useless for astronomical purposes. Not only did they gain or lose time, but they did so in an irregular and unpredictable manner. Could a pendulum be hooked up to the escape mechanism of a clock so as to regulate it?
In 1641, at the age of 77, totally blind, Galileo turned his attention to this problem. Vincenzo Viviani describes the events as follows, as translated by Stillman Drake:
One day in 1641, while I was living with him at his villa in Arcetri, I remember that the idea occurred to him that the pendulum could be adapted to clocks with weights or springs, serving in place of the usual tempo, he hoping that the very even and natural motions of the pendulum would correct all the defects in the art of clocks. But because his being deprived of sight prevented his making drawings and models to the desired effect, and his son Vincenzio coming one day from Florence to Arcetri, Galileo told him his idea and several discussions followed. Finally they decided on the scheme shown in the accompanying drawing, to be put in practice to learn the fact of those difficulties in machines which are usually not foreseen in simple theorizing.
Viviani wrote this in 1659, seventeen years after Galileo’s death and two years after the publication of Christiaan Huygens’s Horologium, in which Huygens described his pendulum clock. It is from Huygens’s construction that we date the practical development of the device.
The Sector
Image of sector use with cannon to measure elevation / Institute and Museum of the History of Science, Florence
As the cannon (introduced in about 1325) became more sophisticated and movable, instruments were developed to help the gunner. To measure the elevation of the barrel, the gunner’s compass was introduced in the sixteenth century. It consisted of two arms at right angles, like a carpenter’s square, and a circular scale between them, on which a plumb line indicated the elevations. Other mathematical instruments developed during this time included compasses, or dividers, that had various useful scales on their legs. Galileo combined the uses of both types of instruments, designing a proportional compass or sector that had many useful scales engraved on its legs and could be used for a variety of purposes, including gunnery.
Galileo’s proportional compass (sector) / Institute and Museum of the History of Science, Florence
Many of Galileo’s students were members of the European nobility who needed to learn a variety of practical subjects besides the more traditional ones. To these students, many of whom lived in his house, he taught fortification, surveying, cosmography, and the use of the sector. Galileo wrote an instruction manual for his sector and in 1598 he installed an instrument maker, Marcantonio Mazzoleni, in his house to produce the sector. His students now bought their own sectors, along with the manuals, from Galileo and received his private instruction on the subject.
Portion of sector ruler / Institute and Museum of the History of Science, Florence
It is not likely that Galileo made a lot of money from this venture, but it illustrates his entrepeneurial efforts in the face of pressing financial responsibilities as the oldest male of his family.
The Thermometer
Galileo’s thermoscope / Institute and Museum of the History of Science, Florence
At the start of the seventeenth century there was no way to quantify heat. In Aristotelian matter theory, heat and cold were fundamental qualities. Like dry and wet, heat and cold were qualities combined with “prima materia” to make up the elements, earth, water, air, and fire. Thus earth was dry and cold, fire dry and hot, etc. Although one might speak of “degrees of heat or cold,” there was no formal distinction between what we would call the extensive concept of heat and the intensive concept of temperature. Also these degrees were not measured, except perhaps in a very rough way as when a physician put his hand on a patient’s forehead and diagnosed “fever heat.”
Measuring heat became a puzzle in the circle of practical and learned men in Venice to which Galileo belonged. The first solution was a thermoscope. Building on Pneumatics by Hero of Alexandria (1st century BCE), first published in the West in 1575, several authors had begun playing with the idea of the expansion of air as its heat increased, and vice versa. The first versions, usually called thermoscopes, were little more than toys. Benedetto Castelli wrote in 1638 about a device he had seen in Galileo’s hands around 1603:
He took a small glass flask, about as large as a small hen’s egg, with a neck about two spans long [perhaps 16 inches] and as fine as a wheat straw, and warmed the flask well in his hands, then turned its mouth upside down into the a vessel placed underneath, in which there was a little water. When he took away the heat of his hands from the flask, the water at once began to rise in the neck, and mounted to more than a span above the level of the water in the vessel. The same Sig. Galileo had then made use of this effect in order to construct an instrument for examining the degrees of heat and cold.
Over the next several years this thermoscope was developed by Santorio Santorio and Galileo’s friend Gianfrancesco Sagredo (both in Venice), Galileo, and others to include a numerical scale. It had thus become a full-fledged air thermometer. The first series of quantitative meteorological observations date from this period. In other parts of Europe the inventor Cornelis Drebbel and Robert Fludd developed similar instruments. The questions about who was the first, and whether one derived his knowledge from another, are sterile ones which shed little light on the historical context in which this and other instruments (e.g., the telescope and barometer) developed. The near simultaneous (and surely independent) invention of the air thermometer illustrates the seventeenth-century trend toward quantification of natural phenomena–an essential dimension of the “mathematization of nature.”
Galileo demonstrating the thermoscope / Institute and Museum of the History of Science, Florence
The liquid in glass thermometer was developed in the 1630s, but a universal standard of temperature remained elusive. Each scientist had his own scale divisions, often based on different reference points. It is impossible for us accurately to convert their measurements to our temperature scale, and at the time it was impossible to compare temperatures in different places. In the early eighteenth century, universal temperature scales based on several fiduciary points (e.g. a mixture of ice and brine, a mixture of ice and water, body temperature, the boiling point of water) were developed by Daniel Gabriel Fahrenheit (1686-1736), Anders Celsius (1701-1744), and Ren\x{00E9}-Antoine Ferchault de Reaumur (1683-1757). Of these, the first two are still in use, and the system of Celsius (extended to become an absolute scale in the nineteenth century) has become the standard scientific temperature scale.
Telescope
Johannes Hevelius observing with one of his telescopes. / Selenographia, 1647
The telescope was one of the central instruments of what has been called the Scientific Revolution of the seventeenth century. It revealed hitherto unsuspected phenomena in the heavens and had a profound influence on the controversy between followers of the traditional geocentric astronomy and cosmology and those who favored the heliocentric system of Copernicus. It was the first extension of one of man’s senses, and demonstrated that ordinary observers could see things that the great Aristotle had not dreamed of. It therefore helped shift authority in the observation of nature from men to instruments. In short, it was the prototype of modern scientific instruments. But the telescope was not the invention of scientists; rather, it was the product of craftsmen. For that reason, much of its origin is inaccessible to us since craftsmen were by and large illiterate and therefore historically often invisible.
Although the magnifying and diminishing properties of convex and concave transparent objects was known in Antiquity, lenses as we know them were introduced in the West at the end of the thirteenth century. Glass of reasonable quality had become relatively cheap and in the major glass-making centers of Venice and Florence techniques for grinding and polishing glass had reached a high state of development. Now one of the perennial problems faced by aging scholars could be solved. With age, the eye progressively loses its power to accommodate, that is to change its focus from faraway objects to nearby ones. This condition, known as presbyopia, becomes noticeable for most people in their forties, when they can no longer focus on letters held at a comfortable distance from the eye. Magnifying glasses became common in the thirteenth century, but these are cumbersome, especially when one is writing. Craftsmen in Venice began making small disks of glass, convex on both sides, that could be worn in a frame–spectacles. Because these little disks were shaped like lentils, they became known as “lentils of glass,” or (from the Latin) lenses. The earliest illustrations of spectacles date from about 1350, and spectacles soon came to be symbols of learning.
The Spectacle Vendor by Johannes Stradanus, engraved by Johannes Collaert, 1582
These spectacles were, then, reading glasses. When one had trouble reading, one went to a spectacle-maker’s shop or a peddler of spectacles and found a suitable pair by trial and error. They were, by and large, glasses for the old. spectacles for the young, concave lenses that correct the refractive error known as myopia, were first made (again in Italy) in the middle of the fifteenth century. So by about 1450 the ingredients for making a telescope were there. The telescopic effect can be achieved by several combinations of concave and convex mirrors and lenses. Why was the telescope not invented in the fifteenth century? There is no good answer to this question, except perhaps that lenses and mirrors of the appropriate strengths were not available until later.
In the literature of white magic, so popular in the sixteenth century, there are several tantalizing references to devices that would allow one to see one’s enemies or count coins from a great distance. But these allusions were cast in obscure language and were accompanied by fantastic claims; the telescope, when it came, was a very humble and simple device. It is possible that in the 1570s Leonard and Thomas Digges in England actually made an instrument consisting of a convex lens and a mirror, but if this proves to be the case, it was an experimental setup that was never translated into a mass-produced device.
The earliest known illlustration of a telescope. Giovanpattista della Porta included this sketch in a letter written in August 1609.
The telescope was unveiled in the Netherlands. In October 1608, the States General (the national government) in The Hague discussed the patent applications first of Hans Lipperhey of Middelburg, and then of Jacob Metius of Alkmaar, on a device for “seeing faraway things as though nearby.” It consisted of a convex and concave lens in a tube, and the combination magnified three or four times. The gentlemen found the device too easy to copy to award the patent, but it voted a small award to Metius and employed Lipperhey to make several binocular versions, for which he was paid handsomely. It appears that another citizen of Middelburg, Sacharias Janssen had a telescope at about the same time but was at the Frankfurt Fair where he tried to sell it.
Galileo’s telescope / Institute and Museum of the History of Science, Florence
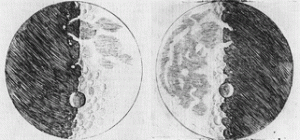
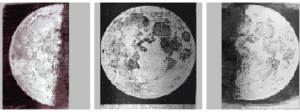
The news of this new invention spread rapidly through Europe, and the device itself quickly followed. By April 1609 three-powered spyglasses could be bought in spectacle-maker’s shops on the Pont Neuf in Paris, and four months later there were several in Italy. We know that Thomas Harriot observed the Moon with a six-powered instrument early in August 1609. But it was Galileo who made the instrument famous. He constructed his first three-powered spyglass in June or July 1609, presented an eight-powered instrument to the Venetian Senate in August, and turned a twenty-powered instrument to the heavens in October or November. With this instrument he observed the Moon, discovered four satellites of Jupiter, and resolved nebular patches into stars. He published Sidereus Nuncius in March 1610.
Verifying Galileo’s discoveries was initially difficult. In the spring of 1610 no one had telescopes of sufficient quality and power to see the satellites of Jupiter, although many had weaker instruments with which they could see some of the lunar detail Galileo had described in Sidereus Nuncius. Galileo’s lead was one of practice, not theory, and it took about six months before others could make or obtain instruments good enough to see Jupiter’s moons. With the verification of the phases of Venus by others, in the first half of 1611, Galileo’s lead in telescope-making had more or less evaporated. The next discovery, that of sunspots, was made by several observers, including Galileo, independently.
Spyglass construction / Institute and Museum of the History of Science, Florence
A typical Galilean telescope with which Jupiter’s moons could be observed was configured as follows. It had a plano-convex objective (the lens toward the object) with a focal length of about 30-40 inches., and a plano-concave ocular with a focal length of about 2 inches. The ocular was in a little tube that could be adjusted for focusing. The objective lens was stopped down to an aperture of 0.5 to 1 inch. , and the field of view was about 15 arc-minutes (about 15 inches in 100 yards). The instrument’s magnification was 15-20. The glass was full of little bubbles and had a greenish tinge (caused by the iron content of the glass); the shape of the lenses was reasonable good near their centers but poor near the periphery (hence the restricted aperture); the polish was rather poor. The limiting factor of this type of instrument was its small field of view–about 15 arc-minutes–which meant that only a quarter of the full Moon could be accommodated in the field. Over the next several decades, lens-grinding and polishing techniques improved gradually, as a specialized craft of telescope makers slowly developed. But although Galilean telescopes of higher magnifications were certainly made, they were almost useless because of the concomitant shrinking of the field.
As mentioned above, the telescopic effect can be achieved with different combinations of lenses and mirrors. As early as 1611, in his Dioptrice, Johannes Kepler had shown that a telescope could also be made by combining a convex objective and a convex ocular. He pointed out that such a combination would produce an inverted image but showed that the addition of yet a third convex lens would make the image erect again. This suggestion was not immediately taken up by astronomers, however, and it was not until Christoph Scheiner published his Rosa Ursina in 1630 that this form of telescope began to spread. In his study of sunspots, Scheiner had experimented with telescopes with convex oculars in order to make the image of the Sun projected through the telescope erect. But when he happened to view an object directly through such an instrument, he found that, although the image was inverted, it was much brighter and the field of view much larger than in a Galilean telescope. Since for astronomical observations an inverted image is no problem, the advantages of what became known as the astronomical telescope led to its general acceptance in the astronomical community by the middle of the century.
The Galilean telescope could be used for terrestrial and celestial purposes interchangeably. This was not true for the astronomical telescope with its inverted image. Astronomers eschewed the third convex lens (the erector lens) necessary for re-inverting the image because the more lenses the more optical defects multiplied. In the second half of the seventeenth century, therefore, the Galilean telescope was replaced for terrestrial purposes by the “terrestrial telescope,” which had four convex lenses: objective, ocular, erector lens, and a field lens (which enlarged the field of view even further).
Left: Hevelius’s 60 foot telescope, Right: Hevelius’s 140 foot telescope / From Machina Coelestis, 1673
With the acceptance of the astronomical telescope, the limit on magnification caused by the small field of view of the Galilean telescope was temporarily lifted, and a “telescope race” developed. Because of optical defects, the curvature of lenses had to be minimized, and therefore (since the magnification of a simple telescope is given roughly by the ratio of the focal lengths of the objective and ocular) increased magnification had to be achieved by increasing the focal length of the objective. Beginning in the 1640s, the length of telescopes began to increase. From the typical Galilean telescope of 5 or 6 feet in length, astronomical telescopes rose to lengths of 15 or 20 feet by the middle of the century. A typical astronomical telescope is the one made by Christiaan Huygens, in 1656. It was 23 feet long; its objective had an aperture of several inches, it magnified about 100 times, and its field of view was 17 arc-minutes.
Aerial telescope / From Christiaan Huygensm Astroscopium Compendiaria,1684
Telescopes had now again reached the point where further increases in magnification would restrict the field of view of the instrument too much. This time another optical device, the field lens came to the rescue. Adding a third convex lens–of appropriate focal length, and in the right place–increased the field significantly, thus allowing higher magnifications. The telescope race therefore continued unabated and lengths increased exponentially. By the early 1670s, Johannes Hevelius had built a 140-foot telescope.
But such long telescopes were useless for observation: it was almost impossible to keep the lenses aligned and any wind would make the instrument flutter. After about 1675, therefore, astronomers did away with the telescope tube. The objective was mounted on a building or pole by means of a ball-joint and aimed by means of a string; the image was found by trial and error; and the compound eyepiece (field lens and ocular), on a little stand, was then positioned to receive the image cast by the objective. Such instruments were called aerial telescopes.
Although some discoveries were made with these very long instruments, this form of telescope had reached its limits. By the beginning of the eighteenth century very long telescopes were rarely mounted any more, and further increases of power came, beginning in the 1730s, from a new form of telescope, the reflecting telescope.
Since it was known that the telescopic effect could be achieved using a variety of combinations of lenses and mirrors, a number of scientists speculated on combinations involving mirrors. Much of this speculation was fueled by the increasingly refined theoretical study of the telescope. In his Dioptrique, appended to his Discourse on Method of 1637, Renè Descartes addressed the problem of spherical aberration, already pointed out by others. In a thin spherical lens, not all rays from infinity–incident parallel to the optical axis–are united at one point. Those farther from the optical axis come to a focus closer to the back of the lens than those nearer the optical axis. Descartes had either learned the sine law of refraction from Willebrord Snell (Snell’s Law) or had discovered it independently, and this allowed him to quantify spherical aberration. In order to eliminate it, he showed, lens curvature had to be either plano-hyperboloidal or spherico-ellipsoidal. His demonstration led many to attempt to make plano-hyperboloidal objectives, an effort which was doomed to failure by the state of the art of lens-grinding. Others began considering the virtues of a concave paraboloidal mirror as primary receptor: it had been known since Antiquity that such a mirror would bring parallel incident rays to a focus at one point.
Newton’s reflecting telescope (1671)
A second theoretical development came in 1672, when Isaac Newton published his celebrated paper on light and colors. Newton showed that white light is a mixture of colored light of different refrangibility: every color had its own degree of refraction. The result was that any curved lens would decompose white light into the colors of the spectrum, each of which comes to a focus at a different point on the optical axis. This effect, which became known as chromatic aberration, resulted in a central image of, e.g., a planet, being surrounded by circles of different colors. Newton had developed his theory of light several years before publishing his paper, when he had turned his mind to the improvement of the telescope, and he had despaired of ever ridding the objective of this defect. He therefore decided to try a mirror, but unlike his predecessors he was able to put his idea into practice. He cast a two-inch mirror blank of speculum metal (basically copper with some tin) and ground it into spherical curvature. He placed it in the bottom of a tube and caught the reflected rays on a 45° secondary mirror which reflected the image into a convex ocular lens outside the tube. He sent this little instrument to the Royal Society, where it caused a sensation; it was the first working reflecting telescope. But the effort ended there. Others were unable to grind mirrors of regular curvature, and to add to the problem, the mirror tarnished and had to be repolished every few months, with the attending danger of damage to the curvature.
Hevelius’s rooftop observatory / From Machina Coelestis, 1673
The reflecting telescope therefore remained a curiosity for decades. In second and third decades of the eighteenth century, however, the reflecting telescope became a reality in the hands of first James Hadley and then others. By the middle of the century, reflecting telescopes with primary mirrors up to six inches in diameter had been made. It was found that for large aperture ratios (the ratio of focal length of the primary to its aperture, as the f-ratio in modern cameras for instance), f/10 or more, the difference between spherical and paraboloidal mirrors was negligible in the performance of the telescope. In the second half of the eighteenth century, in the hands of James Short and then William Herschel, the reflecting telescope with parabolically ground mirrors came into its own.
Observations, Experiments, and Discoveries
The Moon
The Moon in Sidereus Nuncius
Ignoring the occasional pre-telescopic appearance of exceptionally large sunspots, the Moon is the only heavenly body which shows features to the naked eye–the Man in the Moon. These features are permanent, and it was therefore obvious that the Moon always keeps its same face turned to us (although there are minor perturbations that were not noticed until later). In the philosophy of Aristotle (384-322 BCE), these features presented somewhat of a problem. The heavens, starting at the Moon, were the realm of perfection, the sublunary region was the realm of change and corruption, and any resemblance between these regions was strictly ruled out. Aristotle himself suggested that the Moon partook perhaps of some contamination from the realm of corruption.
Although Aristotle’s natural philosophy was very influential in the Greek world, it was not without competitors and skeptics. Thus, in his little book On the Face in the Moon’s Orb, the Greek writer Plutarch (46-120 CE) expressed rather different views on the relationship between the Moon and Earth. He suggested that the Moon had deep recesses in which the light of the Sun did not reach and that the spots are nothing but the shadows of rivers or deep chasms. He also entertained the possibility that the Moon was inhabited. In the following century, the Greek satirist Lucian (120-180 CE) wrote of an imaginary trip to the Moon, which was inhabited, as were the Sun and Venus.
The medieval followers of Aristotle, first in the Islamic world and then in Christian Europe, tried to make sense of the lunar spots in Aristotelian terms. Various possibilities were entertained. It had been suggested already in Antiquity that the Moon was a perfect mirror and that its markings were reflections of earthly features, but this explanation was easily dismissed because the face of the Moon never changes as it moves about the Earth. Perhaps there were vapors between the Sun and the Moon, so that the images were actually contained in the Sun’s incident light and thus reflected to the Earth. The explanation that finally became standard was that there were variations of “density” in the Moon that caused this otherwise perfectly spherical body to appear the way it does. The perfection of the Moon, and therefore the heavens, was thus preserved.
It is a curious fact that although many symbolic images of the Moon survive in medieval and Renaissance works of art (usually a crescent), virtually no one bothered to represent the Moon with its spots the way it actually appeared. We only have a few rough sketches in the notebooks of Leonardo da Vinci (ca. 1500) and a drawing of the naked-eye moon by the English physician William Gilbert. None of these drawings found its way into print until well after the telescope had come into astronomy.
The telescope delivered the coup de grace to attempts to explain away the Moon’s spots and to the perfection of the heavens in general. With his telescope, Galileo saw not only the “ancient” spots, but many smaller ones never seen before. In these smaller spots, he saw that the width of the dark lines defining them varied with the angle of solar illumination. He watched the dark lines change and he saw light spots in the unilluminated part of the Moon that gradually merged with the illuminated part as this part grew. The conclusion he drew was that the changing dark lines were shadows and that the lunar surface has mountains and valleys. The Moon was thus not spherical and hardly perfect.
Galileo’s wash drawings
Galileo was not the only observer of the Moon. Indeed, he was not the first. Thomas Harriot drew the first telescopic representation of the Moon and observed our nearest neighbor for several years. His drawings, however, remained unpublished.
Those who wished to defend the perfection of the heavens brought out the old argument about rarity and density. In the letter of the Collegio Romano mathematicians to Cardinal Bellarmine of April 1611, Christoph Clavius (74 years old) expressed a minority opinion: “But it appears to Father Clavius more probable that the surface is not uneven, but rather that the lunar body is not of uniform density and has denser and rarer parts, as are the ordinary spots seen with the natural sight.” The other three Jesuit mathematicians on the faculty of the college, however, believed that the lunar surface was indeed uneven. In this case the opposition faded away over the next few years.
Galileo wrote in a letter, 1610, that he would like to make a series of representations of the Moon showing its changing phases. Presumably his purpose was to show how the shadows of individual features changed with the illumination. It appears that he abandoned this plan when he saw that there was no need for such an ambitious and expensive project: even the Jesuit fathers in Rome were convinced that the Moon’s surface was uneven. Indeed, Galileo never returned to the task of representing the Moon. (In the 1630s he did, however, observe lunar librations [the real or apparent oscillatory motion of the moon], which show that the Moon does not always keep exactly the same face turned toward the Earth.) Others did little better. Thomas Harriot did make a rough map of the full Moon but never published it. Representations by Christoph Scheiner, Giuseppe Biancani, and Charles Malapert were little more than diagrams, useful only for supporting the verbal argument that the Moon’s surface is rough and uneven. These were, so to speak, generic moons, not portraits of our nearest neighbor.
Sketches of the Moon by Scheiner (1614), Biancani (1620) and Malapert (1619)
If early observations and representations of the Moon were designed to address the issue of its mountainous nature and affinity with the Earth, by the 1630s the accent was shifting. The rough lunar surface was now accepted by astronomers and they turned their attention to how telescopic observations could help them solve the problem of longitude. A lunar eclipse is an event that appears the same to all observers for whom the Moon is above the horizon (which is, of course, not the case with solar eclipses). As the Moon enters the Earth’s shadow cone, one can mark the times at which the shadow crosses a particular feature and later compare this time with the (local) time at which a distant colleague observed the same event. The difference in local times translates directly into their difference in longitude. But a verbal description of the lunar feature under consideration was not enough. A lunar map was needed on which specific features could be unambiguously identified. In Aix and Provence, Nicholas Claude Fabri de Peiresc (still interested in the problem of longitude) and his friend, the astronomer Pierre Gassendi, decided to make a moonmap. They engaged the services of Claude Mellan, one of the foremost artists and engravers of his age. With Gassendi’s sketches and guidance, Mellan engraved three view of the Moon, first quarter, full Moon, and last quarter.
Claude Mellan’s moon engravings.
Mellan’s three engravings are surely the finest artistic renderings of the Moon ever made, but they show an artist’s Moon, not an astronomer’s Moon. Mellan wonderfully represented what he saw through the telescope: at first and last quarter the details at the edge of the Moon are washed out while the features near the terminator stand out starkly; conversely, at full Moon the features in the center are washed out while those near the edge show prominent relief. Where the solar rays are perpendicular to the lunar surface they cast no shadows, but where they rake the surface they throw long shadows. What astronomers needed was a single map that showed all the features equally clearly–a composite view that pictured the Moon in a way it never appeared in reality but was accurate in its placement of individual features.
The first such map was made by the Belgian cosmographer and astronomer Michael Florent van Langren in 1645. Two years later a much more influential effort was published by Johannes Hevelius. In 1647 Hevelius, a wealthy brewer in the Polish city of Gdansk, published Selenographia, the first treatise entirely devoted to the Moon. Hevelius combined all the talents necessary for his task. He made his own lenses, constructed his own telescopes, observed the Moon on every clear night for several years, drew his observations, engraved them himself, and had the wealth to publish a sumptuous book at his own expense. In Selenographia he presented engravings of every conceivable phase of the Moon as well as three large plates of the full Moon: one of the ways the full Moon actually appeared through the telescope, one the way a maker of terrestrial maps might represent it (using the conventions of geographers), and one a composite map of all lunar features illuminated (impossibly) from the same side. It is this last map that was to be used by astronomers during lunar eclipses. Hevelius also suggested a system of nomenclature based on earthly features.
Hevelius founded the science of selenography (after Selene, the goddess of the Moon) and showed astronomers how to represent heavenly bodies. Selenographia was a model for all who came after him. All lunar maps since his time have used the convention of single illumination (although while he used morning illumination modern maps use evening illumination after van Langren’s model). He also instituted the practice of showing the entire lunar surface visible from the Earth, which, because of librations, is greater than a hemisphere. Hevelius’s nomenclature, although used in Protestant countries until the eighteenth century, was replaced by the system published in 1651 by the Jesuit astronomer Giovanni Battista Riccioli, who gave the large naked-eye spots the names of seas (Sea of Tranquillity, Sea of Storm, etc.) and the telescopic spots (now called craters) the name of philosophers and astronomers. It should be pointed out that although Riccioli wrote his Almagestum Novum (“New Almagest”) in which this map appeared to combat the Copernican theory, he was evenhanded in assigning names: Copernicus and Kepler were assigned prominent craters, and even Galileo received his due.
One last note. As the astronomical telescope with its inverted image came into use, astronomers quickly adopted the habit of representing the way they saw the Moon–upside down. This practice was followed until very recently. Lunar images are now constructed and stored digitally and can be displayed in any orientation. Astronomers have therefore reverted to showing the Moon right side up.
Sunspots

Sunspots are dark areas of irregular shape on the surface of the Sun. Their short-term and long-term cyclical nature has been established in the past century. Spots are often big enough to be seen with the naked eye. While direct observation of the Sun in a clear sky is painful and dangerous, it is feasible when the Sun is close to the horizon or when it is covered by a thin veil of clouds or mist. Records of naked-eye sunspot observations in China go back to at least 28 BCE. In the West, the record is much more problematical. It is possible that the Greek philosopher Anaxagoras observed a spot in 467 BCE, and it appears that there are a few scattered mentions in the ancient literature as well. However, in the dominant Aristotelian cosmology, the heavens were thought to be perfect and unchanging. A spot that comes and goes on the Sun would mean that there is change in the heavens. Given this theoretical predisposition, the difficulty of observing the Sun, and the cyclic nature of spots, it is little wonder that records of sunspots are almost non-existent in Europe before the seventeenth century. A very large spot seen for no less than eight days in 807 was simply interpreted as a passage of Mercury in front of the Sun. Other mentions of spots seen on the Sun were ignored by the astronomers and philosophers. In 1607 Johannes Kepler wished to observe a predicted transit of Mercury across the Sun’s disk, and on the appointed day he projected the Sun’s image through a small hole in the roof of his house (a camera obscura – a darkened boxlike device in which images of external objects, received through an aperture, are exhibited in their natural colors on a surface arranged to receive them) and did indeed observe a black spot that he interpreted to be Mercury. Had he been able to follow up on his observation the next day, he would still have seen the spot. Since he knew that Mercury takes only a few hours to cross the Sun’s disk during one of its infrequent transits, he would have known that what he observed could not have been Mercury.

Sunspot
The scientific study of sunspots in the West began after the telescope had been brought into astronomy in 1609. Although there is still some controversy about when and by whom sunspots were first observed through the telescope, we can say that Galileo and Thomas Harriot were the first, around the end of 1610; that Johannes and David Fabricius and Christoph Scheiner first observed them in March 1611, and that Johannes Fabricius was the first to publish on them. His book, De Maculis in Sole Observatis (“On the Spots Observed in the Sun”) appeared in the autumn of 1611, but it remained unknown to the other observers for some time.

Harriot’s sunspot drawings
In the meantime, Galileo had shown sunspots to a number of people in Rome during his triumphant visit there in the spring of 1611. But although some of his corespondents began making regular observations a few months later, Galileo himself did not undertake a study of sunspots until April 1612. Scheiner began his serious study of spots in October 1611 and his first tract on the subject, Tres Epistolae de Maculis Solaribus Scriptae ad Marcum Welserum (“Three Letters on Solar Spots written to Marc Welser”) appeared in January 1612 under the pseudonym “Apelles latens post tabulam,” or “Apelles waiting behind the painting.” Welser was a scholar and banker in Augsburg, who was a patron of local scholars.

Sunspot plate from Scheiner’s Tres Epistolae
Scheiner, a Jesuit mathematician at the university of Ingolstadt (near Augsburg), wished to preserve the perfection of the Sun and the heavens and therefore argued that sunspots were satellites of the Sun. They appeared as black spots when they passed in front of the Sun but were invisible at other points in their orbits. Their orbits had to be very close to the Sun for their shapes were foreshortened as they approached its edge. Scheiner observed sunspots through a telescope equipped with colored glasses.
In the winter of 1611-12, when Galileo received a copy of Scheiner’s tract from Welser along with a request for his comments, he was ill, and what little energy he had he was devoting to the publication of his Discourse on Bodies in Water. When, however, that book was at the printer’s, in April 1612, he turned his attention to sunspots with the help of his protege Benedetto Castelli, who was in Florence at the time. It was Castelli who developed the method of projecting the Sun’s image through the telescope, a technique that made it possible to study the Sun in detail even when it was high in the sky. Galileo wrote his first letter to Welser on sunspots, in which he argued that spots were, in fact, on the surface of the Sun or in its atmosphere, and although he could not say for certain what they were, they appeared to him most like clouds.
While Scheiner wrote in Latin, Galileo wrote his letter in Italian, and Welser had to have it translated before Scheiner could read it. Scheiner had continued his solar observations, and by the time he had mastered Galileo’s letter he had already finished two more letters of his own to Welser. He now added a third, in which he commented that his observations agreed precisely with those of Galileo and defended his judgment that sunspots were solar satellites. This second series of letters was published by Welser in October 1612 under the title De Maculis Solaribus . . . Accuratior Disquisitio (“A More Accurate Disquisition . . . on Sunspots”). Scheiner maintained his pseudonym of Apelles “or, if you prefer, Odysseus under the shield of Ajax.” In the meantime, Galileo had written a second letter to Welser in August 1612. In this letter he showed a large number of sunspot observations, made at roughly the same time of the day, so that the Sun’s orientation was the same and the motion of the spots across its disk could be easily followed. Upon receiving Scheiner’s second tract he wrote yet a third, dated December 1612, attacking Apelles’s opinions once again. At the end of his last letter Galileo mentioned the Copernican System favorably in a way that some scholars have interpreted as his first endorsement of that theory.

“Helioscopium” used by Scheiner for his later sunspot observations
Galileo’s three letters were published in Rome by the Lyncean Academy in the summer of 1613. About a third of the copies had reprints of the two tracts by Apelles (whose identity had in the meantime become known) in their original Latin. There was little doubt about the winner of this contest. Scheiner’s language was convoluted, and not only did Galileo demolish his argument, he also criticized Scheiner’s a priori method of argument: the Sun is perfect, therefore it cannot have spots on its surface.
Up to this point, relations between Galileo and Scheiner were not strained. Scheiner had treated Galileo with great respect, and Galileo had been courteous in his language. Ten years later, in his Assayer, Galileo complained about those who would steal his priority of discovery, mentioning the case of sunspots but not mentioning Scheiner. It is almost certain that Galileo was complaining about several others who had published on sunspots but who had not recognized his priority. Scheiner, who at this time was settling in Rome, took Galileo’s complaint to be directed at him and became Galileo’s sworn enemy.



Sunspot drawings from Scheiner’s Rosa Ursina
Scheiner had in the meantime published several important books on optics, and he had continued his study of the Sun. He published his results in a massive tome, Rosa Ursina, (“The Rose of Orsini”), which became the standard treatise on sunspots for over a century. Scheiner had abandoned his opinion that spots were solar satellites, and he indeed came out in favor of the system of Tycho Brahe and abandoned the perfection of the heavens. His method of illustrating the motion of individual spots across the face of the Sun became the standard way of rendering this motion and the changing shapes of the spots.

Sunspot drawing by Gassendi
After this time, however, sunspot activity was drastically reduced. When, in 1671, a prominent sunspot was observed, it was treated as a rare event. Sunspot activity increased again after about 1710. The period of low activity is now referred to as the Maunder Minimum, after Edward Walter Maunder (1851-1928), one of the first modern astronomers to study the long-term cycles of sunspots. Modern studies of sunspots originated with the rise of astrophysics, around the turn of the century. The chief early investigator of these phenomena in the United States was George Ellery Hale (1868-1938), who built the first spectro-heliograph and built the Yerkes and Mount Wilson observatories, including the 200-inch telescope on Palomar Mountain.


Sunspots drawings by Hevelius
Satellites of Jupiter

Jupiter’s moons
Jupiter has a large number of satellites. Of these, four are comparable to the Earth’s Moon in size; the rest are orders of magnitude smaller. When Jupiter is at opposition and closest to the Earth, the stellar magnitude of its four large moons is between 5 and 6. This means that, were it not for the shielding brightness of Jupiter, these bodies would be visible with the naked eye. The aperture of the telescope used by Galileo in 1610 and its magnification thus brought these four “Galilean” satellites within his grasp.
But first Galileo had to make adjustments to the instruments. When viewing bodies that are very bright and very small, the optical defects of the telescope can be crippling. By trial and error Galileo learned to stop down the aperture of his instrument until he could begin to make useful observations. At the end of 1609, as he was finishing his series of observations of the Moon, Jupiter was at opposition and the brightest object in the evening sky (not counting the Moon). When he had made the new adjustment to his instrument, he turned his attention to Jupiter. On 7 January 1610 he observed the planet and saw what he thought were three fixed stars near it, strung out on a line through the planet. This formation caught his attention, and he returned to it the following evening.
Galileo’s expectation was that Jupiter, which was then in its retrograde loop, would have moved from east to west and had left the three little stars behind. Instead, he saw all three stars to the west of Jupiter. It appeared as though Jupiter had not moved to the west but rather to the east. This was an anomaly, and Galileo returned to this formation again and again. Over the next week he found out several things. First, the little stars never left Jupiter; they appeared to be carried along with the planet. Second, as they were carried along, they changed their position with respect to each other and Jupiter. Third, there were not three but four of these little stars. By the 15th of January he had figured it out: these were not fixed stars but rather planetary bodies that revolved around Jupiter. Jupiter had four moons. His book, Sidereus Nuncius, in which his discovery was described, came off the press in Venice in the middle of March 1610 and made Galileo famous.


Galileo’s observations of Jupiter’s moon
The moons of Jupiter had a major impact on cosmology. In 1610 the traditional Aristotelian cosmology had come under attacks from Copernican astronomers. Aristotelians had a number of arguments against the Copernican System, one of which was now made obsolete. In traditional cosmology, there was only one center of motion, the center of the universe which was the place of the Earth. The motions of all heavenly bodies centered on the Earth. But according to the Copernican theory, the Earth went around the Sun while the Moon went around the Earth. There were thus two centers of motion, which seemed an absurdity. Moreover, if the Earth was a planet, like Mercury, Venus, Mars, Jupiter, and Saturn, why was it the only planet to have a Moon? Galileo’s discovery answered this question. The Earth was, in fact, not the only planet to have a moon, Jupiter had four. And no matter what cosmological system one believed in, there were now at least two centers of motion in the universe, the Earth or Sun and Jupiter. Thus, although the satellites (the term was first used by Johannes Kepler) of Jupiter were by no means proof of the truth of the Copernican system, they certainly added ammunition on that side of the argument.
In the purely astronomical realm, the satellites of Jupiter posed a new problem for astronomers. It had taken centuries in Antiquity to arrive at adequate geometrical modes for the motions of the known planets. Now there was a new system of planetary bodies in miniature, and astronomers had to develop models that could predict their motions. There was a great incentive to come up with good mathematical models, for the satellites offered some hope for the solution of the problem of longitude at sea. It took almost two centuries, however, before the models and tables based on them reached satisfactory accuracy.
The naming of the satellites provides an interesting example of how such matters were handled before the foundation of the International Astronomical Union in the twentieth century. As their discoverer, Galileo claimed the right to name the satellites. He wanted to name them after his patrons and asked whether they would prefer “Cosmic Stars” (after Cosimo II) or “Medicean Stars.” They opted for the latter, and through much of the seventeenth century they were known by that name. In his notebooks, Galileo referred to them individually by number, starting with the satellite closest to Jupiter, but he never had occasion to refer to them in this way in print.
In Provence, Nicholas Claude Fabri de Peiresc tried to differentiate between the Medicean Stars by assigning them the names of individual members of the family, but this system was not published and thus was never used by others. In his Mundus Iovialis (“Jovian World”) of 1614, Simon Marius went into the naming problem in some depth. First, he himself used the numerical system beginning with the satellite closest to Jupiter. Second, he thought that he might call them after his patron, the Duke of Brandenburg — a suggestion followed by no one. Third, he suggested naming the farthest satellite the Saturn of Jupiter, the next one the Jupiter of Jupiter, the third one the Venus of Jupiter, and the one nearest the planet the Mercury of Jupiter. This cumbersome system never caught on. Finally, Marius related a suggestion by Kepler:
Jupiter is much blamed by the poets on account of his irregular loves. Three maidens are especially mentioned as having been clandestinely courted by Jupiter with success. Io, daughter of the River, Inachus, Callisto of Lycaon, Europa of Agenor. Then there was Ganymede, the handsome son of King Tros, whom Jupiter, having taken the form of an eagle, transported to heaven on his back, as poets fabulously tell . . . . I think, therefore, that I shall not have done amiss if the First is called by me Io, the Second Europa, the Third, on account of its majesty of light, Ganymede, the Fourth Callisto . . . .
This fancy, and the particular names given, were suggested to me by Kepler, Imperial Astronomer, when we met at Ratisbon fair in October 1613. So if, as a jest, and in memory of our friendship then begun, I hail him as joint father of these four stars, again I shall not be doing wrong.
None of these suggestion caught on because with Jupiter’s satellites, there was no confusion in the numbering system. Following Galileo and Marius, astronomers simply referred to them by number. With the satellites of Saturn, however, a problem developed. In 1655 Huygens discovered the first and largest; then in 1671-72 Giandomenico Cassini discovered two more, and in 1684 yet another two. These five satellites were numbered like their Galilean counterparts. But when in 1789 William Herschel discovered two additional satellites internal to the first, confusion followed. Did one now renumber them all (thus causing confusion for those who consulted older works), refer to the two new ones as nos. 6 and 7 (thus making the order of the satellites confusing), or refer to them by order of discovery (equally confusing as to order)? Herschel’s son, John Frederick William, suggested in 1847 that Saturn’s satellites be given individual names of mythological figures associated with Saturn after the suggestion made by Marius for Jupiter’s satellites. When, the following year, William Lassel and George Bond independently discovered an eighth satellite of Saturn, they agreed to adopt the naming system proposed by Herschel, in which Saturn’s satellites were named after his brothers and sisters, the Titans. This system and the now revived suggestion by Kepler and Marius for Jupiter quickly became the convention for naming the satellites of the superior planets.








Galilean satellites
Saturn

To all serious observers of the heaven, it was known that stars move in a fixed formation around the Earth except for seven bodies that moved through the fixed stars in a wide band, the zodiac. To the Greeks, all heavenly bodies were stars; most were fixed but some wandered. These seven wandering stars, or planets, were (in the conventional order), Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn. Mercury was the most difficult to observe because it was always close to the Sun, Venus, as morning or evening star, was the brightest body in the heavens. Mars had a distinctive red color, Jupiter at opposition was very bright, and the straw-colored Saturn, the slowest of all planets (sidereal period – a period determined by or from the stars – of 30 years), was the dimmest. The planets were identified with gods by the Mesopotamians, and the Greeks copied this system, assigning planets the names of their gods. The planets were also associated with the seven known metals: Moon/silver, Mercury/mercury, Venus/copper, Sun/gold. Mars/iron, Jupiter/tin, and Saturn/lead. In accordance with their gods, the planets were assigned astrological meanings still used by the astrologers who write daily columns in many of our newspapers.

Saturn as the Grim Reaper
Saturn, associated with time and the grim reaper, was usually depicted with a scythe. According to the prevailing cosmology of Aristotle, Western astronomers knew that, like all other heavenly bodies, the planet Saturn was perfect and spherical. The telescope therefore gave them a surprise. After publishing Sidereus Nuncius, in March 1610, Galileo continued scrutinizing the heavens, especially the planets, in the hope of making further discoveries. In July, as Saturn was bright in the evening sky and approaching opposition,1 he turned his telescope toward it and made a new discovery. On 30 July he wrote to his Medici patron:
I discovered another very strange wonder, which I should like to make known to their Highnesses . . . , keeping it secret, however, until the time when my work is published . . . . the star of Saturn is not a single star, but is a compsite of three, which almost touch each other, never change or move relative to each other, and are arranged in a row along the zodiac, the middle one being three times larger than the lateral ones, and they are situated in this form: oOo.
Galileo no doubt planned to publish this new discovery in his next book, but in the meantime, how could he preserve his priority and prevent others from claiming the discovery as their own? His solution was to circulate an anagram, s m a i s m r m i l m e p o e t a l e u m i b u n e n u g t t a u i r a s. Others would know that he had discovered something and when he had discovered it, but they would not known what the discovery was. The number of letters in the anagram, 37, was too small to allow him later to fudge and change the solution to describe a discovery made by someone else in the meantime. Before the days of scientific papers (invented in the 1660s) this was an effective (if not always foolproof) method of claiming priority.
Galileo sent his correspondents the solution of the anagram, Altissimum planetam tergeminum observavi, or “I have observed the highest planet tri-form. And the newly configured Saturn now took its place in Galileo’s Hall of Fame. But there was something very strange about this planet. For one thing, after being notified other observers often saw the planet oval shaped, but Galileo argued that this was due to inferior telescopes. For another, if these lateral bodies were satellites, they were very different from the satellites of Jupiter for they were much larger with respect to the planet and never moved with respect to it. Or did they?
In his third sunspot letter, dated December 1612, Galileo revealed another mystery about the planet: the lateral bodies had disappeared. Although Galileo confidently predicted that they would return, which they did, Saturn’s appearances remained an enigma. If Saturn was sometimes seen oval (denied by Galileo), sometimes with two lateral bodies, and at other times round and solitary, how could one explain all these appearances? And the mystery grew deeper as time went on. In 1616 Galileo announced to his patrons that he had now observed Saturn in yet another shape, and he published this without commentary in his Asayer of 1623.


Galileo’s sketch of 1616 and engraving in The Assayer of 1623.
Although the planet had again appeared solitary in 1626, few noticed this. But by the next solitary appearance in 1642, there was a growing community of telescopic astronomers who now made observation of the planet a central part of their research programs. Pierre Gassendi and Johannes Hevelius played central roles in this quest, but there were a number of others. Astronomers now routinely published figures of the shapes in which they had observed Saturn. Near the solitary appearances, virtually all astronomers still saw the planet triple-bodied as Galileo had first seen it; at other times, however, they saw two arms, or handles (Latin, ansae) attached to the central body and, representations of this handled appearance varied greatly.

The composite figure from Huygens’s Systema Saturnium
If in 1642 there was a lack of information about Saturn’s appearances, by 1655 when the handles had again shrunk into little disks and the planet was approaching its solitary appearance, there was a plethora of information. What was needed now was a model or theory that would make sense out of all these divergent observations. In 1656 Hevelius pubished De Nativa Saturni Facie (On the Real Appearance of Saturn”), in which he proposed that Saturn’s body was ellipsoidal in shape with two crescents attached to its extremeties. Rotation about the minor axis in the plane of the crescents would, according to Hevelius, explain all the planet’s appearances.

Havelius’s Theory
His book convinced few. In 1658 Christopher Wren (remembered more for his later architecture) proposed a model in which a “corona” so thin it could be considered a mere surface was attached to the planet; the entire formation rotated or librated about its major axis.
In the meantime, Christiaan Huygens had discovered a satellite of Saturn, now named Titan. In 1656 he published a brief tract on the discovery and included an anagram containing his own theory about Saturn’s appearances. He unveiled his theory in 1659, in a substantial book entitled Systema Saturnium (“The Saturnian System”). Huygens’s theory was that the planet was surrounded by a thin flat ring that nowhere touched it. Although Huygens did think that the ring had an appreciable thickness, this was basically the modern solution of the problem.

Wren’s Theory
But Huygens’s solution was a geometrical one. The question now facing astronomers was how such a ring could be stable. Huygens thought the ring was a solid structure; others opined that it was made up of a huge swarm of minute satellites. The argument went on for several centuries until James Clerk Maxwell published his mathematical analysis of the ring structure in 1858, proving that the ring had to be made up of particles no larger than a few inches. At the end of the nineteenth century, spectrographic studies showed that the angular rotation of the inside of the ring was greater than that of the outside of the ring, and that the ratio obeyed Kepler’s third law. The problem was now solved, although Saturn’s ring system still held surprises, as can be seen from the results of the recent flybys of the planet.

Huygen’s Theory
Tides
What is the cause of the tides? In the age of Galileo, this question had many answers, from animistic concepts about the “breath” of the earth, to the pre-Newtonian intuition that the moon should have something to do with the sea’s motions. But Galileo saw this problem in a different way, connecting it to the whole structure of the Copernican universe. In 1597 the Pisan scientist wrote a letter to Kepler, saying that he had found in the Copernican doctrine a way to explain many natural phenomena1, perhaps (as Kepler supposed, referring to Galileo’s letter) even a puzzling one, like that of the tides. What, exactly, the Galilean solution to the problem of the tides was, became clear only in 1616, when Galileo was in Rome, trying to convince the Church not to ban the Copernican theory. After this attempt failed, with the consequence that the Copernican position could no longer be held or defended, Galileo wrote his “Discorso sul flusso e il reflusso del mare”, in the form of a private letter to Cardinal Orsini3.
In this letter Galileo examines in how many ways the water contained in a vase can move. A first way derives from the slope of the vase, like that of the bed of a river. Secondly, an external cause (such as a strong wind) can produce waves in the water. But there is also a third cause for the water to move: the motion of the vase itself. Indeed, if the vase has an irregular motion (i.e. with accelerations and decelerations), the water also acquires a motion. Galileo makes a comparison between the water and the seas and between the vase and the earth, so that the changes in the motions of the sea can be effects of an irregularity in the earth motion. Galileo’s theory is based on the following reasoning: the Copernican earth is affected by two main circular motions, i. e. the annual revolution around the sun and the diurnal rotation. Due to a additive effect of these motions, there is an alteration in the surface speed of the earth, every 12 hours. Referring to the diagram, in which the large circle represents the earth’s annual orbit and the small circle the earth itself, Galileo explained his ideas as follows:
[W]hile the circle BCDL turns on itself in the direction BCD, there are in its circumference mutually contrary movements: for, while the parts near C go down, the opposite ones near L go up; and while the parts near B move toward the left, the part on the opposite side near D move toward the right. Thus, in a complete rotation the point marked B first moves down and toward the left; when it is near C, it descends the most and begins to move toward the right; at D it no longer goes down, but moves most toward the right and begins to go up; and at L it ascends the most, begins to move slowly toward the left, and goes up till B. Now let us combine the specific motions of the parts of the earth with the general movement by the whole globe through the circumference AFG. We shall find that the absolute motion of the upper part (near B) is always fastest, resulting from the composition of the annual motion along the circumference AF and the specific motion of the part B, which two motions reinforce each other and add up toward the left; on the other hand, the absolute motion of the lower parts near D is always slowest, since the specific motion of D, which here is fastest toward the right, must be subtracted from the annual motion along the circumference AF, which is toward the left. . . .
Thus, for 12 hours, a point on the earth’s surface will move eastward, in opposition to the global westward movement of the earth, and for 12 hours it will move westward, in the same direction as the annual motion. The composition of these motions causes on one hand a slackening (due to a subtraction of two opposite motions) and on the other hand an acceleration (due to an addition of two motions in the same direction).

With this mechanism, Galileo thought he had found the irregularity in the movement of the vase (the earth), able to move the water (the seas). Although this irregularity is not perceived by us on solid ground, Galileo was sure it was shown by the oceans, by the ebb and flow of the tides. Galileo intended to solve two problems at the same time: the tides are not a mystery any more if we consider them an effect of the earth’s motions, and the earth’s motions themselves (i.e. the Copernican system) are not absurd any more if we consider the tides a tangible proof of these motions.
Such a theory remained in Galileo’s mind until 1623, when Maffeo Barberini, who was considered a friend and a patron of artists and scientists, became Pope (Urban VIII). Galileo tried to propose again the Copernican question, and obtained the permit to write a dialogue, in which to discuss the arguments for the two main world systems (Ptolemaic and Copernican), without presenting a final verdict. Galileo worked for almost 10 years at the Dialogue: it is divided in four Days in which Salviati (a Copernican) and Simplicio (an Aristotelian) confront each other; a third character (Sagredo) listens to them, often intervening in favor of Salviati. In the Fourth Day of this masterpiece appears the theory of the tides again, the proof that the earth’s motions are not a fiction, that the fluctuations of the sea are effects of mechanical causes and not of a magical attraction between the moon and the water. The earth is a planet: all that happens on it is caused by its own motions, not by the astral influences. This proof, however, presented the final verdict that the Pope did not want the Dialogue to contain: Galileo was brought before the Inquisition and again lost his battle.
Many critical questions are involved in this Galileo theory of the tides: first of all the fact that, rejecting any kind of attractive force as the real cause of the tides, this theory was, in Newtonian terms, an error. Nevertheless this judgment has for a long time impeded a historical evaluation of Galileo’s theory. Only in some recent essays the question is examined with more care and is judged in the context of the physical and astronomical debate of the seventeenth century. To accuse Galileo of an excess of scientific realism, or even of presumption (as some authors have done), is to lose the possibility of historical reconstruction in which what counts is not the achievement of the future, but the efforts to reach them. Galileo was trying to build a scientific method in a world based more on books than on the nature, more on astrology than on astronomy, more on closing one’s eyes than on observing through the telescope. That his theory of the tides did not survive the critical judgment of his successors is not germane to historical inquiry.
Comets

Comet Ikeya-Seki
Comets played an important role in the revolution of astronomy and cosmology that occurred between 1500 and 1700. In the earlier Aristotelian geocentric cosmological scheme, the universe was divided into two regions with very different characteristics. The heavens, which reached from the sphere of the Moon to that of the fixed stars, were perfect and unchanging; motion there was exclusively circular. Below the Moon was the world of corruption and change. The Earth was the center of the universe, the natural place of all heavy bodies (bodies in which the element earth predominated). Around it were arranged in successive spherical shells the elements of water, air, and fire. The sphere of fire reached up to the sphere of the Moon, the first heavenly sphere. Although there are references in Aristotle that some of the imperfection of the sublunary region may have rubbed off on the Moon, basically the divide between the heavenly and sublunary regions was absolute.
If the heavens were perfect and unchanging, then no change could occur in them. Any phenomenon that involved change was, therefore, by definition a sublunary one. Whereas heavenly bodies moved around the Earth in never ending circles, repeating their patterns over and over, comets came and went. They appeared suddenly, moved across the constellations for a brief period of time, and then disappeared. There was no regularity, no pattern to their appearances and motions. They were therefore considered changing appearances and therefore by definition their location was “below” the Moon. (It is to be noted here that this is true only in western cosmology after Aristotle. In the cosmologies of other cultures, comets were defined differently.)
The Aristotelian cosmology was dominant in the Islamic world and in Christian Europe. We find no coherent record of comets in the astronomical annals of these cultures (as we do, for instance in China). Comets were, of course, observed, and they are mentioned in chronicles and other non-astronomical documents. They were considered omens, bad omens, and since there was always a major disaster (plague, war, flood, fire, etc.) that happened shortly after a comet had been seen, there was no easy way to prove this notion wrong.

Comet of 1449-50 observed by Toscanelli
The first recorded efforts to study the paths of comets across the heavens as an astronomical exercise occurred in Florence in the fifteenth century, about a century before the birth of Galileo. By the early sixteenth century, astronomers were observing and measuring the positions of all comets, and in the 1530s Peter Apian in Germany discovered that the tail of a comet always points away from the Sun. His discovery was illustrated in a tract written in German, meant for popular consumption. Among the philosophers (and cosmology was a part of philosophy) there was as yet no doubt that comets were sublunary phenomena.

Comet of 1532 observed by Apian
But practicing astronomers, that is those who observed the positions of heavenly bodies and calculated their positions, increasingly began to measure the positions of comets. If they were below the Moon, then their parallax (change in the position of an object in the heavens due to the orbit of the earth. Observable parallax in the fixed stars is a proof of the rotation of the earth around the sun) could be no less than the Moon’s, about 1 degree (the horizontal parallax, which is the angle subtended at the Moon by the Earth’s radius). Why did not a few carefully executed measurements settle this issue quickly?
First, there was in Europe no great tradition of making accurate, or even regular, astronomical observations before about 1500. For that reason, measuring instruments were primitive, not even taking advantage of the capabilities of existing technology. They were simple, hand-held, wooden instruments–little more than roughly calibrated sticks–and their accuracy was perhaps at best 1/4 degree, usually perhaps 1/2 degree. There was little accuracy and even less consistency in the measurements of individual astronomers. When it came to comparing the measurements of practitioners in places all over Europe, the situation became hopeless. The results were parallaxes ranging from 10 degree to negative values.
Second, astronomers and others who practiced the mathematical sciences dealt only with positions and motions. These were accidental properties of bodies and could tell you nothing about their essences. A mathematician could tell you where the apple was and he could describe its motion if it fell. But this information could not tell you what made this body an apple and why it fell. These were questions that belonged to philosophy. It was therefore not at all obvious that the measurements of the astronomers could turn an obviously changing cometary phenomenon into a perfect and immutable heavenly body.

Comet of 1577
By the time Galileo was beginning to turn his attention to the study of mathematics, the science of astronomy was changing. Copernicus’s De Revolutionibus (1543) had been around for a generation, and there were other cosmological theories as well that challenged the existing cosmology. When in 1577 a huge comet appeared whose tail spread in a great arc across the sky, observers all over Europe, Tycho Brahe among them, made measurements of its changing positions. The resulting literature was huge, and if the verdict was by no means unanimous, it was clear that the opinion that comets were heavenly bodies had become respectable in learned circles. The rising authority of Tycho Brahe, based on his noble birth and his miraculous instruments, gave added impetus to the change of opinion. Over the next two generations the perfection of the heavens was abandoned, as were the crystalline spheres of which they were supposedly composed.

Comet of 1618
But placing comets in the heavens raised new questions. What were their paths? What was their nature? Through much of the seventeenth century the debate ranged. in his Assayer of 1623 Galileo argued that comets were optical phenomena and that therefore one could not measure their parallaxes. In this opinion he was not followed by others. It was argued that comets moved in straight lines or parabolic arcs. Descartes argued that comets were bodies that traveled from one solar system to another.
The mechanical philosophy of the second half of the seventeenth century had a great bearing on this debate, as we can see in Isaac Newton’s conclusions. In his Mathematical Principles of Natural Philosophy of 1687, Newton argued that all matter attracts all other matter. If comets are made of matter, then they are attracted to the Sun just as the planets are. Given rectilinear inertia and a centrally directed force, the moving body’s path must be a conic section. Edmond Halley took this notion and drew up a table of the parameters of the twenty-odd brightest comets that had been seen over the previous several centuries. He pointed out that the parameters of the comets of 1533, 1607 and 1682 were the same and concluded that this was a periodic comet. He predicted its return in 1758. In that year (Halley had died in 1742) the comet appeared as predicted and has been called Halley’s Comet ever since.
Longitude at Sea

Until the end of the fifteenth century, sailors navigated with almost daily reference to land. In the Mediterranean it was difficult to go very far astray, and in western and northwest Europe navigation was coastal. Ships hugged the shore from Gibraltar to the Norway and the Baltic. The only exception to this rule was the trade between Scandinavia, Iceland, and occasionally Greenland. These routes were discovered (probably by accident) by the Vikings around 1000 CE. With the Portuguese voyages of discovery, in the fifteenth century, navigation became more difficult. For some time Portuguese sailors hugged the coast of Africa, as they carefully explored the contours of this continent. Both the winds and the currents there made sailing south difficult, however, and beginning with the voyages of Diaz (who rounded the Cape of Good Hope) in 1486, Columbus in 1492, and da Gama in 1498, Spanish and Portuguese sailors sailed the high seas for weeks on end without seeing land. How did they know where they were and whether they were on the right course?
Until the end of the fifteenth century, sailors navigated with almost daily reference to land. In the Mediterranean it was difficult to go very far astray, and in western and northwest Europe navigation was coastal. Ships hugged the shore from Gibraltar to the Norway and the Baltic. The only exception to this rule was the trade between Scandinavia, Iceland, and occasionally Greenland. These routes were discovered (probably by accident) by the Vikings around 1000 CE. With the Portuguese voyages of discovery, in the fifteenth century, navigation became more difficult. For some time Portuguese sailors hugged the coast of Africa, as they carefully explored the contours of this continent. Both the winds and the currents there made sailing south difficult, however, and beginning with the voyages of Diaz (who rounded the Cape of Good Hope) in 1486, Columbus in 1492, and da Gama in 1498, Spanish and Portuguese sailors sailed the high seas for weeks on end without seeing land. How did they know where they were and whether they were on the right course?
The only reference points on the high seas were the stars and Sun. Locations and courses now had to be spatial: a navigator needed to locate himself on a grid of imaginary lines of latitude and longitude.
The Portuguese pioneered the method of navigating by latitude. Ships had to be equipped with instruments (astrolabes, cross staffs) to measure the altitudes of stars or the Sun. It was not difficult to determine one’s latitude to within about a degree by this method. Longitude was, however, a different matter. Observations of the Sun and stars were of no immediate help: in order to determine one’s longitude with respect to, e.g., Lisbon, one had to find out the difference in local times between one’s location and Lisbon. No easy method that was sufficiently accurate suggested itself. The magnitude of the problem is illustrated by the voyage of the Portuguese navigator Cabral who, on his way to the East Indies, swung west in the south Atlantic in order to pick up favorable winds and ran into the coast of Brazil. Further, the world maps prepared in the sixteenth century erred widely in the longitudes of places. The east-west length of the Mediterranean was in error by 19\x{00B0}–about 1100 miles! The longitudes of China and Japan were off by much larger margins. For nations engaged in trade with the East and West Indies, finding longitude at sea was a matter of national interest. Late in the sixteenth century the Spanish Crown instituted a large prize in the hope of a solution. This initiative was followed by the French, Dutch, and English governments in the seventeenth century.
Soon after the discovery of the satellites of Jupiter, scientists realized that the formation of the satellites provided a clock whose face could be seen from every vantage point. In 1612 Nicholas Claude Fabri de Peiresc in Aix en Provence sent out an observer to the eastern part of the Mediterranean to observe Jupiter’s satellites while he did the same at home. The idea was to compare the satellite positions and formations observed on the same day at Aix and, e.g., Tripoli and from these to deduce the difference in local (solar) times between the two locations. Peiresc was, however, disappointed by the results: the positions of the satellites changed too slowly for this purpose. Had the method been more accurate, he had hoped to provide sailors with tables of the motions of the satellites, so that they could carry the standard time reference with them and determine their longitude on the spot. Peiresc now abandoned this effort.
In 1612 Galileo for the first time observed an eclipse of a satellite of Jupiter. When a satellite enters the shadow cone behind the planet it disappears very quickly. Such eclipses were, for all practical purposes, instantaneous events. If a navigator on the high seas could note the local time of such an eclipse and compare it with the local time at which it was predicted to happen at the European reference location, the difference in times and therefore longitude could easily be found. Could sufficiently accurate tables be drawn up?
In 1613 Galileo entered into negotiations with the Spanish Crown to provide Spanish navigators with eclipse tables for the satellites and telescopes with which to make the observations. He worked for many years to perfect his knowledge of the satellites’ motions but never published his results (presumably because they were not sufficiently accurate). He did, however, have reasonable hopes of being able to predict eclipses over short periods. But there was a more severe problem. In order to observe the satellites, one needed a telescope of relatively high power, say 15, and given the small field of view of the Galilean telescope (perhaps 20′ of arc) it was impossible to make the observation from the deck of a ship on the high seas. Galileo made some trials of a telescope attached to a helmet (he called this device a celatone) on ships riding at anchor in the harbor of Livorno, but this approach only worked with rather low-powered telescopes. The Spanish were not impressed by the method, and negotiations eventually faltered.
Galileo took up the problem again after his trial, and this time he negotiated (through intermediaries) with the States General of the Netherlands, who had just announced their prize. Although the Dutch government admired Galileo greatly, its committee came to the same conclusion its Spanish counterpart had earlier. For his efforts, the States General voted Galileo a gold medal and chain, but Galileo was forbidden by the Inquisition from accepting this award.
By Galileo’s death, in 1642, the only tables of the motions of Jupiter’s satellites were an inaccurate effort published by Simon Marius in 1614. The Sicilian astronomer Giovanni Battista Odierna published new tables in 1654, but these were again not accurate. The first reasonably accurate tabl es were published by Gian Domenico Cassini in 1668.

Gian Domenico Cassini
It was because of Cassini’s tables that the Danish astronomer Olaeus Romer was able, in 1676, to find a systematic error of about 10 minutes, whose period was equal to the synodic period (opposition to opposition) of Jupiter. Romer correctly interpreted his result to demonstrate that light does not travel instantaneously. He estimated that it took eleven minutes for light from the Sun to reach the Earth.

Cassini’s tables of 1668
Tables–especially those of the motion of the first satellites, whose period is about 42 hours and whose eclipses are therefore most frequent–were now becoming sufficiently accurate to hold out hope that they could be used for determining longitude at sea. The English worked hard–using first the newer astronomical telescope with its larger field of view and then, in the eighteenth century, the reflecting telescope–to make it possible for an observer on a ship to observe the satellites. They went so far as to install gimbaled observing seats that were independent of the motion of the ship. But progress was incrementally slow, and in the 1760s a practical solution to the problem of longitude at sea came from the clock-makers: John Harrison had managed to make clocks so accurate and impervious to motion that they could be carried on a ship and not err by more than seconds on a trip to the East Indies. On his first voyage to the South Seas, Captain James Cook took a Harrison chronometer with him and his trials proved this method to be entirely satisfactory.
In the meantime, however, the French had made a different use of satellite eclipses. If it was not feasible to make observations from the deck of a moving ship, it was certainly possible to observe the satellites on land. In the 1670s French astronomers, under the leadership of Cassini, began making observations of the satellites in many locations in France. The resulting map of France, finished in 1679 showed that the west coast of France was too far west by an entire degree on existing maps and that similar adjustments had to be made to the Mediterranean coast. It is said that upon seeing this map, King Louis XIV remarked that he was losing more territory to his astronomers than to his enemies.
The method of determining longitudes by means of observations of the eclipses of Jupiter’s satellites was at the center of the revolution in geodesy in the eighteenth century. Travelers and explorers routinely timed eclipses and sent their results back to Paris and London, to be compared with the observations made there. When Charles Mason and Jeremiah Dixon surveyed the boundary line between Pennsylvania and Maryland, from 1763 to 1767, they used eclipses of the satellites of Jupiter to determine the exact longitudes of places.
Theories
Copernican System

Copernicus
The first speculations about the possibility of the Sun being the center of the cosmos and the Earth being one of the planets going around it go back to the third century BCE. In his Sand-Reckoner, Archimedes (d. 212 BCE), discusses how to express very large numbers. As an example he chooses the question as to how many grains of sand there are in the cosmos. And in order to make the problem more difficult, he chooses not the geocentric cosmos generally accepted at the time, but the heliocentric cosmos proposed by Aristarchus of Samos (ca. 310-230 BCE), which would have to be many times larger because of the lack of observable stellar parallax. We know, therefore, that already in Hellenistic times thinkers were at least toying with this notion, and because of its mention in Archimedes’s book Aristarchus’s speculation was well-known in Europe beginning in the High Middle Ages but not seriously entertained until Copernicus.

Copernicus
European learning was based on the Greek sources that had been passed down, and cosmological and astronomical thought were based on Aristotle and Ptolemy. Aristotle’s cosmology of a central Earth surrounded by concentric spherical shells carrying the planets and fixed stars was the basis of European thought from the 12th century CE onward. Technical astronomy, also geocentric, was based on the constructions of excentric circles and epicycles codified in Ptolemy’s Almagest (2d. century CE).
In the fifteenth century, the reform of European astronomy was begun by the astronomer/humanist Georg Peurbach (1423-1461) and his student Johannes Regiomontanus (1436-1476). Their efforts (like those of their colleagues in other fields) were concentrated on ridding astronomical texts, especially Ptolemy’s, from errors by going back to the original Greek texts and providing deeper insight into the thoughts of the original authors. With their new textbook and a guide to the Almagest, Peurbach and Regiomontanus raised the level of theoretical astronomy in Europe.
Several problems were facing astronomers at the beginning of the sixteenth century. First, the tables (by means of which to predict astronomical events such as eclipses and conjunctions) were deemed not to be sufficiently accurate. Second, Portuguese and Spanish expeditions to the Far East and America sailed out of sight of land for weeks on end, and only astronomical methods could help them in finding their locations on the high seas. Third, the calendar, instituted by Julius Caesar in 44 BCE was no longer accurate. The equinox, which at the time of the Council of Nicea (325 CE) had fallen on the 21st, had now slipped to the 11th. Since the date of Easter (the celebration of the defining event in Christianity) was determined with reference to the equinox, and since most of the other religious holidays through the year were counted forward or backward from Easter, the slippage of the calendar with regard to celestial events was a very serious problem. For the solution to all three problems, Europeans looked to the astronomers.
Nicholas Copernicus (1473-1543) learned the works of Peurbach and Regiomontanus in the undergraduate curriculum at the university of Cracow and then spent a decade studying in Italy. Upon his return to Poland, he spent the rest of his life as a physician, lawyer, and church administrator. During his spare time he continued his research in astronomy. The result was De Revolutionibus Orbium Coelestium (“On the Revolutions of the Celestial Orbs”), which was published in Nuremberg in 1543, the year of his death. The book was dedicated to Pope Paul III and initially caused litle controversy. An anonymous preface (added by Andreas Osiander, the Protestant reformer of Nuremberg) stated that the theory put forward in this book was only a mathematical hypothesis: the geometrical constructions used by astronomers had traditionally had only hypothetical status; cosmological interpretations were reserved for the philosophers. Indeed, except for the first eleven chapters of Book I, De Revolutionibus was a technical mathematical work in the tradition of the Almagest.

Diagram of the Copernican system, from De Revolutions
But in the first book, Copernicus stated that the Sun was the center of the universe and that the Earth had a triple motion around this center. His theory gave a simple and elegant explanation of the retrograde motions of the planets (the annual motion of the Earth necessarily projected onto the motions of the planets in geocentric astronomy) and settled the order of the planets (which had been a convention in Ptolemy’s work) definitively. He argued that his system was more elegant than the traditional geocentric system. Copernicus still retained the priviledged status of circular motion and therefore had to construct his planetary orbits from circles upon and within circles, just as his predecessors had done. His tables were perhaps only marginally better than existing ones.
The reception of De Revolutionibus was mixed. The heliocentric hypothesis was rejected out of hand by virtually all, but the book was the most sophisticated astronomical treatise since the Almagest, and for this it was widely admired. Its mathematical constructions were easily transferred into geocentric ones, and many astronomers used them. In 1551 Erasmus Reinhold, no believer in the mobility of the Earth, published a new set of tables, the Prutenic Tables, based on Copernicus’s parameters. These tables came to be preferred for their accuracy. Further, De revolutionibus became the central work in a network of astronomers, who dissected it in great detail. Not until a generation after its appearance, however, can we begin point to a community of practicing astronomers who accepted heliocentric cosmology. Perhaps the most remarkable early follower of Copernicus was Thomas Digges (c. 1545-c.1595), who in A Perfit Description of the Coelestiall Orbes (1576) translated a large part of Book I of De Revolutionibus into English and illustrated it with a diagram in which the Copernican arrangement of the planets is imbedded in an infinite universe of stars.

Diagram of the universe by Thomas Digges
The reason for this delay was that, on the face of it, the heliocentric cosmology was absurd from a common-sensical and a physical point of view. Thinkers had grown up on the Aristotelian division between the heavens and the earthly region, between perfection and corruption. In Aristotle’s physics, bodies moved to their natural places. Stones fell because the natural place of heavy bodies was the center of the universe, and that was why the Earth was there. Accepting Copernicus’s system meant abandoning Aristotelian physics. How would birds find their nest again after they had flown from them? Why does a stone thrown up come straight down if the Earth underneath it is rotating rapidly to the east? Since bodies can only have one sort of motion at a time, how can the Earth have several? And if the Earth is a planet, why should it be the only planet with a moon?
For astronomical purposes, astronomers always assumed that the Earth is as a point with respect to the heavens. Only in the case of the Moon could one notice a parallactic displacement (about 1°) with respect to the fixed stars during its (i.e., the Earth’s) diurnal motion. In Copernican astronomy one now had to assume that the orbit of the Earth was as a point with respect to the fixed stars, and because the fixed stars did not reflect the Earth’s annual motion by showing an annual parallax, the sphere of the fixed stars had to be immense. What was the purpose of such a large space between the region of Saturn and that of the fixed stars?

Parallax
These and others were objections that needed answers. The Copernican system simply did not fit into the Aristotelian way of thinking. It took a century and a half for a new physics to be devised to undegird heliocentric astronomy. The works in physics and astronomy of Galileo and Johannes Kepler were crucial steps on this road.
There was another problem. A stationary Sun and moving Earth also clashed with many biblical passages. Protestants and Catholics alike often dismissed heliocentrism on these grounds. Martin Luther did so in one of his “table talks” in 1539, before De Revolutionibus had appeared. (Preliminary sketches had circulated in manuscript form.) In the long run, Protestants, who had some freedom to interpret the bible personally, accepted heliocentrism somewhat more quickly. Catholics, especially in Spain and Italy, had to be more cautious in the religious climate of the Counter Reformation, as the case of Galileo clearly demonstrates. Christoph Clavius, the leading Jesuit mathematician from about 1570 to his death in 1612, used biblical arguments against heliocentrism in his astronomical textbook.
The situation was never simple, however. For one thing, late in the sixteenth century Tycho Brahe devised a hybrid geostatic heliocentric system in which the Moon and Sun went around the Earth but the planets went around the Sun. In this system the elegance and harmony of the Copernican system were married to the solidity of a central and stable Earth so that Aristotelian physics could be maintained. Especially after Galileo’s telescopic discoveries, many astronomers switched from the traditional to the Tychonic cosmology. For another thing, by 1600 there were still very few astronomers who accepted Copernicus’s cosmology. It is not clear whether the execution of Giordano Bruno, a Neoplatonist mystic who knew little about astronomy, had anything to do with his Copernican beliefs. Finally, we must not forget that Copernicus had dedicated De Revolutionibus to the Pope. During the sixteenth century the Copernican issue was not considered important by the Church and no official pronouncements were made.
Galileo’s discoveries changed all that. Beginning with Sidereus Nuncius in 1610, Galileo brought the issue before a wide audience. He continued his efforts, ever more boldly, in his letters on sunspots, and in his letter to the Grand Duchess Christina (circulated in manuscript only) he actually interpreted the problematical biblical passage in the book of Joshua to conform to a heliocentric cosmology. More importantly, he argued that the Bible is written in the language of the common person who is not an expert in astronomy. Scripture, he argued, teaches us how to go to heaven, not how the heavens go. At about the same time, Paolo Antonio Foscarini, a Carmelite theologian in Naples, published a book in which he argued that the Copernican theory did not conflict with Scripture. It was at this point that Church officials took notice of the Copernican theory and placed De Revolutionibus on the Index of Forbidden Books until corrected.
Galileo’s Dialogue Concerning the Two Chief World Systems of 1632 was a watershed in what had shaped up to be the “Great Debate.” Galileo’s arguments undermined the physics and cosmology of Aristotle for an increasingly receptive audience. His telescopic discoveries, although they did not prove that the Earth moved around the Sun, added greatly to his argument. In the meantime, Johannes Kepler (who had died in 1630) had introduced physical considerations into the heavens and had published his Rudolphine Tables, based on his own elliptical theory and Tycho Brahe’s accurate observations, and these tables were more accurate by far than any previous ones. The tide now ran in favor of the heliocentric theory, and from the middle of the seventeenth century there were few important astronomers who were not Copernicans.
Ptolemaic System

In his Dialogue Concerning the Two Chief World Systems, Ptolemaic and Copernican of 1632, Galileo attacked the world system based on the cosmology of Aristotle (384-322 BCE) and the technical astronomy of Ptolemy (ca. 150 CE).
In his books On the Heavens, and Physics, Aristotle put forward his notion of an ordered universe or cosmos. It was governed by the concept of place , as opposed to space, and was divided into two distinct parts, the earthly or sublunary region, and the heavens. The former was the abode of change and corruption, where things came into being, grew, matured, decayed, and died; the latter was the region of perfection, where there was no change. In the sublunary region, substances were made up of the four elements, earth, water, air, and fire. Earth was the heaviest, and its natural place was the center of the cosmos; for that reason the Earth was situated in the center of the cosmos. The natural places of water, air, and fire, were concentric spherical shells around the sphere of earth. Things were not arranged perfectly, and therefore areas of land protruded above the water. Objects sought the natural place of the element that predominated in them. Thus stones, in which earth predominated, move down to the center of the cosmos, and fire moves straight up. Natural motions were, then, radial, either down or up. The four elements differed from each other only in their qualities. Thus, earth was cold and dry while air was warm and moist. Changing one or both of its qualities, transmuted one element into another. Such transmutations were going on constantly, adding to the constant change in this sublunary region.

Ptolemy
The heavens, on the other hand, were made up of an entirely different substance, the aether 1 or quintessence (fifth element), an immutable substance. Heavenly bodies were part of spherical shells of aether. These spherical shells fit tightly around each other, without any spaces between them, in the following order: Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn, fixed stars. Each spherical shell (hereafter, simply, sphere) had its particular rotation, that accounted for the motion of the heavenly body contained in it. Outside the sphere of the fixed stars, there was the prime mover (himself unmoved), who imparted motion from the outside inward. All motions in the cosmos came ultimately from this prime mover. The natural motions of heavenly bodies and their spheres was perfectly circular, that is, circular and neither speeding up nor slowing down.
It is to be noted about this universe that everything had its natural place, a privileged location for bodies with a particular makeup, and that the laws of nature were not the same in the heavenly and the earthly regions. Further, there were no empty places or vacua anywhere. Finally, it was finite: beyond the sphere of the fixed stars and the prime mover, there was nothing, not even space. The cosmos encompassed all existence.

Christian Aristotelian Cosmos. From Peter Apian, Cosmographia
Now, ingenious as this cosmology was, it turned out to be unsatisfactory for astronomy. Heavenly bodies did, in fact, not move with perfect circular motions: they speeded up, slowed down, and in the cases of the planets even stopped and reversed their motions. Although Aristotle and his contemporaries tried to account for these variations by splitting individual planetary spheres into component spheres, each with a component of the composite motion, these constructions were very complex and ultimately doomed to failure. Furthermore, no matter how complex a system of spheres for an individual planet became, these spheres were still centered on the Earth. The distance of a planet from the Earth could therefore not be varied in this system, but planets vary in brightness, a variation especially noticeable for Venus, Mars, and Jupiter. Since in an unchangeable heaven variations in intrinsic brightness were ruled out, and since spheres did not allow for a variation in planetary distances from the Earth, variations in brightness could not be accounted for in this system.
Thus, although Aristotle’s spherical cosmology had a very long life, mathematicians who wished to make geometrical models to account for the actual motions of heavenly bodies began using different constructions within a century of Aristotle’s death. These constructions violated Aristotle’s physical and cosmological principles somewhat, but they were ultimately successful in accounting for the motions of heavenly bodies. It is in the work of Claudius Ptolemy, who lived in the second century CE, that we see the culmination of these efforts. In his great astronomical work, Almagest, 2 Ptolemy presented a complete system of mathematical constructions that accounted successfully for the observed motion of each heavenly body.
Ptolemy used three basic constructions, the eccentric, the epicycle, and the equant. An eccentric construction is one in which the Earth is placed outside the center of the geometrical construction. Here, the Earth, E, is displaced slightly from the center, C, of the path of the planet. Although this construction violated the rule that the Earth was the center of the cosmos and all planetary motions, the displacement was minimal and was considered a slight bending of the rule rather than a violation. The eccentric in the figure below is fixed; it could also be made movable. In this case the center of the large circle was a point that rotated around the Earth in a small circle centered on the Earth. In some constructions this little circle was not centered in the Earth.
The second construction, the epicycle, is geometrically equivalent to the simple movable eccentric. In this case, the planet moved on a little circle the center of which rotated on the circumference of the large circle centered on the on theEarth. When the directions and speeds of rotation of the epicycle and large circle were chosen appropriately, the planet, as seen from the Earth, would stop, reverse its course, and then move forward again. Thus the annual retrograde motion of the planets (caused, in heliocentric terms by the addition of the Earth’s annual motion to the motion of the planet) could roughly be accounted for.



From Michael J. Crowe, Theories of the World from Antiquity to the Copernican Revolution
But these two constructions did not quite bring the resulting planetary motions within close agreement with the observed motions. Ptolemy therefore added yet a third construction, the equant. In this case, the center of construction of the large circle was separated from the center of motion of a point on its circumference, as shown below, where C is the geometrical center of the large circle (usually called in these constructions the excentric circle) but the motion of the center of the epicycle, P (middle of Figure), is uniform about Q, the equant point (righthand side of Figure).
Ptolemy combined all three constructions in the models of the planets, Sun, and Moon. A typical construction might thus be as in the picture below, where E is the Earth, C the geometric center of the eccentric circle, Q the equant point, F the center of the epicycle, and P the planet. As mentioned before, the eccentric was often not fixed but moved in a circle about the Earth or another point between the Earth and the equant point.

Typical Ptolemaic planetary model, from Michael J. Crowe, Theories of the World from Antiquity to the Copernican Revolution
With such combinations of constructions, Ptolemy was able to account for the motions of heavenly bodies within the standards of observational accuracy of his day. The idea was to break down the complex observed planetary motion into components with perfect circular motions. In doing so, however, Ptolemy violated the cosmological and physical rules of Aristotle. The excentric and epicycle meant that planetary motions were not exactly centered on the Earth, the center of the cosmos. This was, however, a “fudge” that few objected to. The equant violated the stricture of perfect circular motion, and this violation bothered thinkers a good deal more. Thus, in De Revolutionibus (see Copernican System), Copernicus tells the reader that it was his aim to rid the models of heavenly motions of this monstrous construction.
Aristotelian cosmology and Ptolemaic astronomy entered the West, in the twelfth and thirteenth centuries, as distinct textual traditions. The former in Aristotle’s Physics and On the Heavens and the many commentaries on these works; the latter in the Almagest and the technical astronomical literature that had grown around it, especially the work of Islamic astronomers working in the Ptolemaic paradigm. In the world of learning in the Christian West (settled in the universities founded around 1200 CE), Aristotle’s cosmology figured in all questions concerned with the nature of the universe and impinged on many philosophical and theological questions. Ptolemy’s astronomy was taught as part of the undergraduate mathematical curriculum only and impinged only on technical questions of calendrics, positional predictions, and astrology.
Copernicus’s innovations was therefore not only putting the Sun in the center of the universe and working out a complete astronomical system on this basis of this premise, but also trying to erase the disciplinary boundary between the textual traditions of physical cosmology and technical astronomy.
Atomism
The notion that matter is made up of small, indivisible particles goes back to the ancient Greeks. In the sixth century BCE, thinkers began asking questions about what is the basic underlying reality of the world. In view of the constant change we see in the world around us, is there some substratum (physis, hence our word physics) that is constant? If so, is it material or immaterial, accessible through the senses or only through the mind, is it one or many? Over the next several centuries, these questions were answered in several different ways. Some believed that all was change, others that change was illusory. The Pythagoreans thought that the physis was “number” and pioneered the mathematical approach to nature. Their idealist approach was in stark contrast to that of the materialists, among whom the atomists were most prominent. Leucippus of Miletus (ca. 435 BCE) and Democritus of Abdera (ca. 410 BCE) developed the atomic hypothesis. According to them matter can be subdivided only to a certain point, at which only atoms (that which cannot be cut) remain. The world is made up of atoms moving in the void. Atoms differed from each other only in size and shape, and different substances with their distinct qualities were made up of different shapes, arrangements, and positions of atoms. Atoms were in continuous motion in the infinite void and constantly collided with each other. During these collisions they could rebound or stick together because of hooks and barbs on their surfaces. Thus, underlying the changes in the perceptible world, there was constancy (atoms were neither created nor destroyed); change was caused by the combinations and dissociations of the atoms.
Democritus gave some examples of how the atomic hypothesis could account for qualities such as color and taste (sharp tastes are caused by sharp atoms), but on the whole atomism, like other contemporary global theories, remained a general theory. It was criticized by Aristotle (384-322 BCE) for some of its logical inconsistencies1 and for its inability to explain qualities (color, taste, odor, etc.) that we call (after Galileo) secondary qualities. Aristotle’s matter theory was fundamentally qualitative: qualities were built into the fundamental building blocks that made up substances. And against the atomists’ idea of a nature without design or purpose, Aristotle constructed a natural philosophy that made nature a purposeful agent.
In the philosophical system of Epicurus (341-270 BCE), physics was subordinated to ethics. The aim of his philosophy was to overcome irrational fears of natural phenomena and to achieve peace of mind. Epicurus explained natural phenomena by atomism, but he made several modifications to the doctrine in view of Aristotle’s criticisms. He distinguished between physical and mathematical divisibility and gave atoms weight. In his system atoms originally fell through the infinite void with equal speeds, until one swerved by a tiny amount. This was an uncaused event. This swerve caused collisions and swirls of atoms, and thus worlds were formed. The Epicurean ethical system was influential over the next several centuries, and one of its Roman practitioners, Lucretius (first century BCE), wrote a long poem about it, De Rerum Natura (“On the Nature of Things”), from which much of our knowledge about atomism derives.
In the Christian world, nature was seen as the product of a transcendent creator and was therefore fundamentally rational. Aristotelian notions of purpose and order fit the Christian mindset much better. Moreover, in atomism there was an unbridgeable gap between the level of the atoms and the observable phenomena, whereas Aristotelian natural philosophy addressed observable phenomena directly. Aristotle did, however, postulate minima, the theoretical limit of divisibility of substances, and therefore within European Aristotelianism, there was discussion about the meaning of this limit and in some quarters minima took on a corpuscular nature. This train of thought merged with a revived atomism, caused by the recovery of Lucretius’s De Rerum Natura ca. 1415 CE, to give rise to a corpuscular doctrine that provided the material foundation of the mechanistic philosophy of the seventeenth century. We must be careful, however, not to think that all those who sought causal explanations in the minute building blocks of matter were atomists. Thus, Descartes (1596-1650) believed that matter was infinitely divisible and had no weight (or mass).
In his Assayer of 1623, Galileo explained his notion of the difference between those qualities, mostly found by touch, that are inherent in bodies (weight, roughness, smoothness, etc.) and those that are in the mind of the observer (taste, color, etc.)–in other words, the difference between what we call primary and secondary qualities. In this discussion he referred to bodies that “continually dissolve into minute particles” and stated his opinion that “for exciting in us tastes, odors, and sounds there are required in external bodies anything but sizes, shapes, numbers, and slow or fast movements.” An anonymous cleric filed a report with the Inquisition in which he claimed the first citation to show that Galileo was an atomist and the second to be in conflict with the Council of Trent’s pronunciations on the Eucharist. The report did not lead to any action against Galileo.
Galileo’s notions about the constitution of matter emerge in his Discourses on Two New Sciences of 1638. In his discussion of cohesion–what holds matter together–he puts forward the notion that objects are made up of an infinite number of infinitely small particles held together by an infinite number of small vacua. He did not go beyond this point, but it is clear that this “atomism” is almost exclusively mathematical.
On Motion
During the time he taught the mathematical subjects at the university of Pisa (1589-1592), Galileo began a book, De motu (“On motion”), which was never published. In it, we can trace the early development of his ideas concerning motion.
One of the fundamental propositions of Aristotelian philosophy is that there is no effect without a cause. Applied to moving bodies, this proposition dictates that there is no motion without a force. Speed, then is proportional to force and inversely proportional to resistance. This notion is not at all unreasonable if one takes as one’s defining case of motion, say, an ox pulling a cart: the cart only moves if the ox pulls, and when the ox stops pulling the cart stops. For falling bodies, the force is the weight pulling down a body and the resistance is that of the medium, air or water. As the science of motion became somewhat more quantitative in the sixteenth century, some people began to investigate the motion of falling bodies more carefully. Galileo was one of these.
If weight determines the speed of fall, then when two different weights are dropped from a high place the heavier will fall faster and the lighter slower, in proportion to the two weights. A ten pound weight would reach the Earth by the time a one-pound weight had fallen one-tenth as far.
One approach was to speculate: suppose one connected the two weights with a string, what would be the speed of fall? Suppose one tied them together? In the first case the lighter weight would slow down the heavier one and therefore the time of fall would be greater than that of the heavier weight; in the second case there now was a composite body weighing eleven pounds, whose time of fall would be less than that of the ten-pound weight. Perhaps weight was not the determiner of the speed of fall.
But there was another approach, one of experience. Why not drop bodies of different weights and see whether Aristotle’s prediction was correct. As early as 1544, the historian Benedetto Varchi referred to actual tests, which showed that it was not. In a tract written in 1576, Giuseppe Moletti, Galileo’s predecessor in the chair of mathematics at the university of Padua, reported that bodies of the same material but different weight, as well as bodies of the same volume but different material, dropped from a height arrived at the Earth at the same time.
Galileo’s approach to this problem was somewhat different. In De motu he proposed that in free fall bodies dropped with a characteristic uniform speed determined not by their weight but by their specific gravity (not his term). He put this theory to the test by dropping bodies from heights and found that the experiments did not confirm his theory. He states that, in fact, the lighter body (i.e. that of the lower specific gravity) will move ahead of the heavier body at the start of the fall, and that the heavier body then overtakes it and arrives at the bottom slightly earlier.
Scholars have pointed to such passages to support their argument that Galileo did not perform such experiments and that his references to experiments were only rhetorical devices. After all, we all know that in a vacuum all bodies would fall with the same speed and in a medium such as air the heavier body (assuming the two bodies are of the same shape) will fall slightly faster: at no time will the lighter body be ahead of the heavier one. But when Galileo’s supposed experiment was repeated, the results showed that he had described a real experiment. Students dropped spherical balls of wood and iron of equal diameter and the wooden balls invariably moved ahead of the iron balls. The explanation lies in the fact that the heavier iron ball must be clasped in the hand with more force and is therefore released slightly later than the wooden ball.
Obviously, then, Galileo was performing experiments at the very beginning of his investigations into motion, and he took his experimental results seriously. Over the next two decades he changed his ideas and refined his experiments, and in the end he arrived at the law of falling bodies which states that in a vacuum all bodies, regardless of their weight, shape, or specific gravity, are uniformly accelerated in exactly the same way, and that the distance fallen is proportional to the square of the elapsed time.
Christianity
The Inquisition
The Inquisition was a permanent institution in the Catholic Church charged with the eradication of heresies. Unlike many other religions (e.g., Buddhism, Judaism), the Catholic Church has a hierarchical structure with a central bureaucracy. In the early years of the church, there were several competing sects that called themselves Christian. But after the Emperor Constantine I (280?-337 CE) made Christianity the state religion of the Roman Empire and the local administrative structures were pulled together into one hierarchy centered in Rome, doctrinal arguments were settled by Church Councils, beginning with the Council of Nicea in 325 (which formulated the Nicean Creed). Those whose beliefs or practices deviated sufficiently from the orthodoxy of the councils now became the objects of efforts to bring them into the fold. Resistance often led to persecution.
Heresies (from L. haeresis, sect, school of belief) were a problem for the Church from the beginning. In the early centuries there were the Arians and Manicheans; in the Middle Ages there were the Cathari and Waldenses; and in the Renaissance there were the Hussites, Lutherans, Calvinists, and Rosicrucians. Efforts to suppress heresies were initially ad hoc. But in the Middle Ages a permanent structure came into being to deal with the problem. Beginning in the 12th century, Church Councils required secular rulers to prosecute heretics. In 1231, Pope Gregory IX published a decree which called for life imprisonment with salutary penance for the heretic who had confessed and repented and capital punishment for those who persisted. The secular authorities were to carry out the execution. Pope Gregory relieved the bishops and archbishops of this obligation, and made it the duty of the Dominican Order, though many inquisitors were members of other orders or of the secular clergy. By the end of the decade the Inquisition had become a general institution in all lands under the purview of the Pope. By the end of the 13th centuries the Inquisition in each region had a bureaucracy to help in its function.
The judge, or inquisitor, could bring suit against anyone. The accused had to testify against himself/herself and not have the right to face and question his/her accuser. It was acceptable to take testimony from criminals, persons of bad reputation, excommunicated people, and heretics. The accused did not have right to counsel, and blood relationship did not exempt one from the duty to testify against the accused. Sentences could not be appealed Sometimes inquisitors interrogated entire populations in their jurisdiction. The inquisitor questioned the accused in the presence of at least two witnesses. The accused was given a summary of the charges and had to take an oath to tell the truth. Various means were used to get the cooperation of the accused. Although there was no tradition of torture in Christian canon law, this method came into use by the middle of the 13th century. The findings of the Inquisition were read before a large audience; the penitents abjured on their knees with one hand on a bible held by the inquisitor. Penalties went from visits to churches, pilgrimages, and wearing the cross of infamy to imprisonment (usually for life but the sentences were often commuted) and (if the accused would not abjure) death. Death was by burning at the stake, and it was carried out by the secular authorities. In some serious cases when the accused had died before proceedings could be instituted, his or her remains could be exhumed and burned. Death or life imprisonment was always accompanied by the confiscation of all the accused’s property.
Abuses by local Inquisitions early on led to reform and regulation by Rome, and in the 14th century intervention by secular authorities became common. At the end of the 15th century, under Ferdinand and Isabel, the Spanish inquisition became independent of Rome. In its dealings with converted Moslems and Jews and also illuminists, the Spanish Inquisition with its notorious autos-da-fe represents a dark chapter in the history of the Inquisition. In northern Europe the Inquisition was considerably more benign: in England it was never instituted, and in the Scandinavian countries it had hardly any impact.
Pope Paul III established, in 1542, a permanent congregation staffed with cardinals and other officials, whose task it was to maintain and defend the integrity of the faith and to examine and proscribe errors and false doctrines. This body, the Congregation of the Holy Office, now called the Congregation for the Doctrine of the Faith, part of the Roman Curia, became the supervisory body of local Inquisitions. The Pope himself holds the title of prefect but never exercises this office. Instead, he appoints one of the cardinals to preside over the meetings. There are usually ten other cardinals on the Congregation, as well as a prelate and two assistants all chosen from the Dominican order. The Holy Office also has an international group of consultants, experienced scholars of theology and canon law, who advise it on specific questions. In 1616 these consultants gave their assessment of the propositions that the Sun is immobile and at the center of the universe and that the Earth moves around it, judging both to be “foolish and absurd in philosophy,” and the first to be “formally heretical” and the second “at least erroneous in faith” in theology. This assessment led to Copernicus’s De Revolutionibus Orbium Coelestium to be placed on the Index of Forbidden Books, until revised and Galileo to be admonished about his Copernicanism. It was this same body in 1633 that tried Galileo.
The Congregation of the Index
Freedom of thought and written and oral expression is historically a relatively recent development. For those who were the shepherds of Christian souls and whose function it was to get those souls to heaven, the idea that anyone could think and say or write what he/she wanted was an absurdity. Moreover, it was dangerous because it might lead others into error. As early as 170 CE, the Church promulgated a list of genuine books of the New Testament and excluded others from use in religious practice. In 405 CE, Pope Innocent I published a list of forbidden books, and at the end of that century issued a decree that has been called the first Index of Forbidden Books. It listed the genuine books of the Bible, the apocryphal books, and heretical books. Henceforth Popes and Councils periodically published lists of forbidden books.
With the Council of Trent (1545-1563), the Church instituted a permanent institution to deal with this subject. The Congregation of the Inquisition was initially charged with drawing up a complete list of forbidden books. This list, the first general one, was published in 1559; it was the first to be called Index. It was immediately subject to revision by a papal commission, which published its result in 1564, the Tridentine Index. This index also provided rules for censorship. For almost two centuries, the Index was updated periodically without major revisions, but beginning in 1664 the Index listed forbidden books not according to categories but simply alphabetically. In 1757 and 1897 there were major revisions in the general norms governing censorship and prohibition. The last edition of the Index was that of 1948; it was abolished in 1966. The Catholic Church has, however, not relinquished authority to forbid the reading of books that in its judgment are a danger to the faith and morals of Catholics. Further, books listed on the 1948 Index are not automatically permitted reading for Catholics. For many permission from Church authorities is still required.
In the cases of the Copernican System, the Church was slow to act because it did not see immediate danger to the faithful in De Revolutionibus (1543). For one thing, it was written by a member of the Church. Copernicus was a canon in a monastery, and he dedicated his book to Pope Paul III. For another, the book contained a preface (discovered by Kepler not to have been written by Copernicus) that stated that the geocentric system proposed in the book was only a mathematical hypothesis and made no claims about how the universe was really constituted. But with Galileo’s writings, which reached out to a wide audience and brought the argument about Copernicus into the mainstream of educated discourse, the Church acted. In 1616, after 73 years, it placed De Revolutionibus on the Index subject to revision, along with several other books that defended the Copernican System. It is interesting to note that the revisions required in Copernicus’s book were, in terms of the total work, actually very minor. Copies of De Revolutionibus that were in Italy at this time show the revisions: a few deleted passages and a few changes of individual words. None of Galileo’s books were placed on the Index at this time. Kepler’s New Astronomy, his Epitome of Copernican Astronomy, and his World Harmony were quickly placed on the Index. During the proceedings against Galileo in 1633, his Dialogue Concerning the Two Chief Systems of the World was placed on the Index, where it remained until 1824.
Church Figures
Giordano Bruno

Christian Bartholméss, Jordano Bruno (Paris: Libaririe Philosophique de Ladrange, 1846), frontispiece
Filippo Bruno was born in Nola, near Naples, the son of Giovanni Bruno, a soldier, and Fraulissa Savolino. He took the name Giordano upon entering the Dominican order. In the great Dominican monastery in Naples (where Thomas Aquinas had taught), Bruno was instructed in Aristotelian philosophy. His exceptional expertise in the art of memory brought him to the attention of patrons, and he was brought to Rome to demonstrate his abilities to the Pope. During this period he may also have come under the influence of Giovanni Battista Della Porta, a Neapolitan polymath who published an important book on natural magic. Bruno was attracted to new streams of thought, among which were the works of Plato and Hermes Trismegistus, both resurrected in Florence by Marsilio Ficino in the late fifteenth century. Hermes Trismegistus was thought to be a gentile prophet who was a contemporary of Moses. The works attributed to him in fact date from the turn of the Christian era.
Because of his heterodox tendencies, Bruno came to the attention of the Inquisition in Naples and in 1576 he left the city to escape prosecution. When the same happened in Rome, he fled again, this time abandoning his Dominican habit. For the next seven years he lived in France, lecturing on various subjects and attracting the attention of powerful patrons. From 1583 to 1585 he lived at the house of the French ambassador in London. During this period he published the books that are most important for our purposes, Cena de le Ceneri (“The Ash Wednesday Supper”) and De l’Infinito, Universo e Mondi (“On the Infinite Universe and Worlds”), both published in 1584. In Cena de le Ceneri, Bruno defended the heliocentric theory of Copernicus . It appears that he did not understand astronomy very well, for his theory is confused on several points. In De l’Infinito , Universo e Mondi, he argued that the universe was infinite, that it contained an infinite number of worlds, and that these are all inhabited by intelligent beings.
Wherever he went, Bruno’s passionate utterings led to opposition. During his English period he outraged the Oxford faculty in a lecture at the university; upon his return to France, in 1585, he got into a violent quarrel about a scientific instrument. He fled Paris for Germany in 1586, where he lived in Wittenberg, Prague, Helmstedt, and Frankfurt. As he had in France and England, he lived off the munificence of patrons, whom after some time he invariably outraged. In 1591 he accepted an invitation to live in Venice. Here he was arrested by the Inquisition and tried. After he had recanted, Bruno was sent to Rome, in 1592, for another trial. For eight years he was kept imprisoned and interrogated periodically. When, in the end, he refused to recant, he was declared a heretic and burned at the stake.
It is often maintained that Bruno was executed because of his Copernicanism and his belief in the infinity of inhabited worlds. In fact, we do not know the exact grounds on which he was declared a heretic because his file is missing from the records. Scientists such as Galileo and Johannes Kepler were not sympathetic to Bruno in their writings.
Robert Cardinal

Robert Cardinal Bellarmine
Roberto Bellarmino was born into a noble family in Montepulciano in Tuscany. In 1560, he joined the Jesuit order and began his studies at the Collegio Romano, the Jesuit college in Rome. After finishing his course of studies there and studying Thomistic theology at the university of Padua, Bellarmine became the first Jesuit professor at the university of Louvain (in modern Belgium) in 1569 and was ordained as a priest the following year. Situated in the Low Countries where Protestantism was gaining rapidly during this period, the university of Louvain was becomes a bulwark of Catholic orthodoxy. Bellarmine taught theology out of Thomas Acquinas’s Summa Theologica and studied the Scriptures and the Church Fathers in preparation for a major work on theology. During his period at Louvain he wrote a Hebrew grammar and a work on the Church Fathers.
In 1576 Bellarmine was called back to Rome by Pope Gregory XIII to teach theology to English and German missionaries at the Collegio Romano. He taught there until 1588. Toward the end of this period, his most important scholarly work began appearing:
Disputationes de Controversiis Christianae Fidei Adversus Hujus Temporis Haereticos (Disputations about the Controversies of the Christian faith Against the Heretics of this Time) (3 vols, Ingolstadt, 1586-1593). In this work, Bellarmine brought order to the chaos of theological arguments between Catholics and Protestants. Whereas the literature on this subject was marked by heated debates and intemperate statements on both sides, Bellarmine calmly and fairly reviewed the issues. These volumes became a remarkably effective weapon against reform theology, and it has been argued that they occasioned the return of many to the Catholic Church.
In 1588 Bellarmine became the spiritual director of the Collegio Romano. Among his other duties he taught the catechism to students and lay brothers, and his lessons eventually led to Dottrina Cristiani Breve (Brief Christian Doctrine) Rome, 1597), a small catechism for children, and Dichiarazione piX Copiosa della Dottrina Cristiani (A more copious declaration of the Christian doctrine) (Rome, 1598), a catechism for teachers. Approved by Pope Clement XIII, both catechisms became very popular and were translated into many languages. Their popularity lasted well into the twentieth century.
Bellarmine served as rector of the Collegio Romano in 1592, as provincial of the Neapolitan province of the Jesuits in 1594, and papal theologian in 1597. In 1599 he was made a cardinal. From this time forward he was a member of the Roman Congregation and served on many commissions. In 1602 he was consecrated an archbishop and sent by Pope Clement VIII to Capua, where he concerned himself mainly with pastoral duties. In 1605 he was recalled to Rome.
Bellarmine spent much of his time in theological controversies, mostly involving papal power. He engaged in a public debate, a war of books and pamphlets, concerning the divine right of kings with James I of England. The issue of papal power revolved around the theory of the indirect power of the Pope. His spiritual power is direct and primary; he was not, however, without temporal power because he might have to act with regard to temporal things which affected the spiritual ones. This was the Pope’s indirect power, which Bellarmine defended all his adult life.
In 1616 Bellarmine became involved in the Copernican controversy, which was brought to a head by the publication of Paolo Antonio Foscarini’s book defending the Copernican system from the charge that it clashed with the Scriptures. It was he who administered the controversial admonition to Galileo not to hold or defend the Copernican theory.
In a time when cardinals maintained splendid courts, Bellarmine lived a simple and ascetic life, practicing self-sacrifice, poverty, and disinterestedness. Upon the death of Pope Sixtus V in 1590, the Count of Olivares wrote to King Philip III of Spain about possible candidates for the papacy: “Bellarmine is beloved for his great goodness, but he is a scholar who lives only among books and not of much practical ability . . . . He would not do for a Pope, for he is mindful only of the interests of the Church and is unresponsive to the reasons of princes . . . He would scruple to accept gifts . . . I suggest that we exert no action in his favor.” The King agreed.
The process of canonization was begun in 1627. In 1931 Pope Pius XI finally declared Bellarmine a Doctor of the Church.
Tommaso Caccini
Cosimo Caccini was born in Florence and chose the religious life before he had turned fifteen. Caccini chose the Dominican order and entered the monastery of San Marco. Here, a century earlier, Savanarola had been the prior, and the legacy of this monk’s fiery sermons lived on. Caccini soon showed that he had a talent for preaching, and soon after his novitiate he was already preaching Lenten sermons in the church of Santa Maria Novella. As his reputation spread, he was invited by churches in other cities to perform the same office. Caccini was, however, a pale echo of Savanarola: his fanaticism was never divorced from personal ambition for advancement within the Dominican order. By his choice of the name Tommaso, he served notice that he wished to become the new Thomas Aquinas, the order’s (and the Church’s) greatest theologian. In fact, his published works were derivative and third-rate. For his inflammatory sermons he was disciplined by the Archbishop of Bologna as a scandal-maker.
Shortly after Galileo’s arrival in Florence, Caccini fell in with the so-called “Pigeon League,” named after Lodovico delle Colombe,1 an arch-enemy of Galileo. The group included his fellow Dominican Niccolo Lorini and the Archbishop of Florence. Lorini was the first to attack Galileo from the pulpit, toward the end of 1612, but in the face of an uproar among the friends of Galileo quickly wrote a letter of apology. Caccini’s attack was more damaging. Because of the influence of his brother Matteo, Caccini had been prior of the Dominican monastery in Cortona in 1611, where he had been unsuccessful in obtaining the patronage of Cardinal Maffeo Barberini, and he now had further aspirations in Rome. He was in possession of a copy of Galileo’s letter to Benedetto Castelli (which Galileo later expanded into the “Letter to the Grand Duchess Christina”) showing how the Copernican system could be reconciled with the passage in the book of Joshua. Here was Caccini’s chance. On the fourth Sunday of Advent (20 December 1614), he preached a sermon on Joshua in Santa Maria Novella in Florence, attacking Galileo and for his Copernican views. He reputedly ended his sermon with a passage from chapter 1, verse 11 of The Acts of the Apostles, “Viri galilaei, quid statis adspicientes in caelum?” which is rendered in the King James translation as “Ye men of Galilee, why stand ye gazing up into heaven?” an obvious reference to Galileo and his followers.
Caccini got his wish. He became Master and Bachelor of the convent of Santa Maria sopra Minerva in Rome, and the wheels were set in motion that resulted, eighteen months later, in the condemnation of the Copernican theory. Lorini forwarded a mangled copy of Galileo’s letter to Castelli to Rome, and Galileo then sent the correct original version to Rome as well. In March 1615 Caccini appeared on his own initiative before the Inquisition and gave depositions about Galileo and his views. In November, two other clerics mentioned in Caccini’s deposition were examined in Florence. These depositions show how ignorant these men were, in fact, about Galileo’s views. After reviewing the matter, the Holy Office decided not to take any actions other than having Galileo’s letters on sunspots examined by its theological consultants. Their report, in February 1616, made the proposition of a stationary and central Sun formally heretical and the proposition of a non-central moving Earth “at least erroneous in faith.
From correspondence, it appears that Caccini kept working against Galileo behind the scenes, but apparently to no particular effect. His career, however, did progress. He became confessor to the nuns of the convent of Orsina, and then penitentiary at Santa Maria Maggiore in Rome. He was confined for some time in Viterbo, after which, through the help of his brothers, he was allowed to return to Florence where he became a high theologian of the Dominican order. As prior of the famous monastery of San Marco, he was active behind the scene in the events leading up to Galileo’s trial in 1633. Caccini died in Florence in 1648.
Paolo Antonio Foscarini
Little is known about Foscarini’s life. He was born in Montalto Uffugo in Calabria (southern Italy), joined the Carmelite Order, and distinguished himself as a preacher, mathematician, and theologian. He taught philosophy and theology at the university of Messina in Sicily served as the elected provincial of the Carmelite Order in Calabria. He published Ordinationes et Exercitia Quotidiana (“Daily Ordinations and Exercises”) in 1607; Institutionum Omnis Generis Doctrinarum Tomis VII Comprehensarum Syntaxis (“Syntaxis of All Types of Doctrines, Contained in Seven Tomes”) in 1613; and Tratato della Divinatione Naturale Cosmologica (“Treatise on Natural Cosmological Divination”) in 1615.
In that year, he turned his attention to the Copernican System, and there is some evidence that he and Galileo planned a joined strategy on behalf of heliocentric cosmology. As Galileo wrote his “Letter to the Grand Duchess Christina,” Foscarini published in Naples a tract entitled Lettera sopra l’Opinione de’ Pittagorici, e del Copernico della Mobilita della Terra, e Stabilita del Sole, e del Nuove Pittagorica Systema del Mondo (“Letter concerning the Opinion of the Pythagoreans and Copernicus about the Mobility of the Earth and Stability of the Sun, and about the New Pythagorean System of the World”), dedicated to the General of the Carmelite Order. In this work, Foscarini defended the Copernican theory as true and defended it against charges that it conflicted with Scripture. With book in hand, Foscarini went to Rome to defend the Copernican theory personally but left Rome before Galileo’s arrival there. Shortly afterward, the consultants of the Holy Office made their pronouncement on the Copernican theory, and as a result Foscarini’s book was placed on the Index of Forbidden Books (3 March 1616). Foscarini died a few months later in a Carmelite monastery he had founded in his native city of Montalto.