Medieval Armor / Metropolitan Museum of Art
By Dr. Graham N. Askew, Dr. Federico Formenti, Dr. Alberto E. Minetti
Askew – Associate Professor in Muscle Function and Movement, University of Leeds
Formenti – Professor of Life Sciences and Medicine, Kings College London
Minetti – Professor of Medicine, University of Milan
Abstract
In Medieval Europe, soldiers wore steel plate armour for protection during warfare. Armour design reflected a trade-off between protection and mobility it offered the wearer. By the fifteenth century, a typical suit of field armour weighed between 30 and 50 kg and was distributed over the entire body. How much wearing armour affected Medieval soldiers’ locomotor energetics and biomechanics is unknown. We investigated the mechanics and the energetic cost of locomotion in armour, and determined the effects on physical performance. We found that the net cost of locomotion (Cmet) during armoured walking and running is much more energetically expensive than unloaded locomotion. Cmet for locomotion in armour was 2.1–2.3 times higher for walking, and 1.9 times higher for running when compared with Cmet for unloaded locomotion at the same speed. An important component of the increased energy use results from the extra force that must be generated to support the additional mass. However, the energetic cost of locomotion in armour was also much higher than equivalent trunk loading. This additional cost is mostly explained by the increased energy required to swing the limbs and impaired breathing. Our findings can predict age-associated decline in Medieval soldiers’ physical performance, and have potential implications in understanding the outcomes of past European military battles.
Introduction
Body armour has been used as a means of protecting individuals from injury, primarily during military combat, throughout recorded history. Armour design evolved in parallel with weapon design and manufacturing technology, and reflects the trade-off between reducing the risk of injury to the wearer in the event of being struck by a weapon, while retaining mobility in order to avoid being hit and to be able to attack the adversary. In late Medieval Europe, armour was principally constructed from interlocking steel plates. A suit of Medieval field armour (typically 30–50 kg) comprised a substantial fraction of body weight. This weight of armour is similar to the marching loads carried by various infantry units in military campaigns post-WWII [1] (electronic supplementary material, table S1). Load carrying has a considerable effect on the energetic cost of locomotion because of the increased force that must be generated to support the additional mass [2,3], and the increased mechanical work associated with accelerating the additional mass [4]. In contrast to a load carried in a backpack, armour is distributed over the entire body, loading the limbs as well as the head, neck and trunk. The energetic costs of walking and running are determined by the costs associated with supporting body weight and the costs of swinging the limbs [2–8]. Locomotion in armour is expected to be more energetically costly than equivalent loading of the trunk because of the additional mechanical work needed to swing the loaded limbs [3,8]. There are no quantitative data available on the energetic cost of locomotion in armour, which would potentially help historians to interpret the feats of battle.
Fight-interpreters from the Royal Armouries (Leeds, UK), regularly wear replicas of Medieval armour in performances to the general public, and offer a unique opportunity to gain insight into the energetics of locomotion in armour. We determined the oxygen consumption of fight-interpreters during armoured and unloaded walking and running at a range of speeds in order to quantify the effect that wearing armour has on locomotor energetics (figure 1a). We present the mechanical determinants of the measured energetics, and discuss potential implications on Medieval soldiers’ locomotor performance.
Figure 1: (a) Fight interpreter walking in armour; the respirometry mask used to collect exhaled gases can be seen. Photograph by Graham Askew. (b) Effigy of William Martyn (ca 1470–1480), at the Church of Saint Mary in Puddletown, Dorset upon which replica armour used in the study was based. The sabatons, greaves and cuisses are depicted on the lower limbs. Photograph by Joy White.
Material and Methods
Subjects, armour and respirometry
Four male subjects (mean ± s.d., height 175 ± 4 cm, mass 79 ± 10 kg, age 36 ± 4 years), experienced in wearing replica armour, were informed about the research, and consented to participate in the experiments. Each subject had a suit of custom-made replica armour typical of the mid- to late-fifteenth century. These replica armours were of the following types: English 1470–1480; Milanese mid- to late-fifteenth century; Germanic gothic style late-fifteenth century. The mass of the armour (including arming doublet—a padded garment to which parts of the armour are attached with protective mail gussets) averaged 35 ± 5 kg, representing 44 ± 3% of the individual’s body mass.
Respiratory frequency, tidal volume, CO2 production and O2 consumption were measured on a breath-by-breath basis through a portable metabograph (K4 b2; Cosmed srl, Rome, Italy), while subjects either walked or ran on a treadmill (Trimline model T370HR) wearing armour or under unloaded, control conditions. The experimental technique for respiratory measurements is described in detail elsewhere [9]. Before the locomotion experiments, we measured resting O2 consumption while the subjects stood still in the loaded and control conditions. The rate of oxygen consumption () was measured once had stabilized for at least 1 min at a range of speeds (walk 0.5–2.0 m s−1; run 1.7–2. 0 m s−1). The respiratory exchange ratio (RER) was calculated as the ratio of CO2 production to O2 consumption. RER was lower than 1 in all the experimental sets, indicating aerobic conditions, and used to convert the metabolic cost of locomotion from ml O2 into J. The net metabolic cost of locomotion (Cmet; J kg−1 m−1) was calculated as steady-state minus standing O2 consumption (expressed in J kg−1 s−1) and divided by mean speed (m s−1).
Kinematics
During locomotion on the treadmill, subjects (wearing armour and unloaded) were recorded using a high-speed video camera (Kodak Motioncorder) operating at 125 frames per second and shuttered at 1/1000 s. Stride kinematics were characterized at each speed by measuring the swing and stance duration, which were used to calculate stride frequency and duty factor (i.e. the fraction of the stride duration where each foot is in contact with the ground). We also estimated the mechanical internal work associated with swinging the lower limbs per unit mass and distance (WINT; J kg−1 m−1; modified from [10]).
where f is stride frequency,  is progression speed, d is duty factor, a is the fractional distance of the lower limb centre of mass from the hip (taken as 0.447 for both unloaded and loaded conditions), g is the average radius of gyration of the leg as a fraction of leg length (taken as 0.326 for both unloaded and loaded conditions), mL is the estimated lower leg mass (taken as 16.1% Mb), mA is the mass of armour supported below the hip and Mb is body mass. All subjects carried a longsword, which was supported by both hands during locomotion. Consequently, the movements of the upper limbs relative to the centre of mass of the body were small, and therefore, the mechanical internal work associated with swinging the upper limbs was not calculated. The body mass-specific mechanical power (P*) was calculated as
is progression speed, d is duty factor, a is the fractional distance of the lower limb centre of mass from the hip (taken as 0.447 for both unloaded and loaded conditions), g is the average radius of gyration of the leg as a fraction of leg length (taken as 0.326 for both unloaded and loaded conditions), mL is the estimated lower leg mass (taken as 16.1% Mb), mA is the mass of armour supported below the hip and Mb is body mass. All subjects carried a longsword, which was supported by both hands during locomotion. Consequently, the movements of the upper limbs relative to the centre of mass of the body were small, and therefore, the mechanical internal work associated with swinging the upper limbs was not calculated. The body mass-specific mechanical power (P*) was calculated as
Statistics
ANOVA was used to test for differences in net cost of locomotion, stride and breathing mechanics, with speed and between locomotion in armour and unloaded conditions using SPSS (v. 16, Chicago, USA). In our models, speed and loading condition (armoured or unloaded) were treated as independent variables and an identifier for each individual was included as a random factor. Statistical significance was set at p < 0.05. All proportional data were arcsine-transformed prior to analysis. Where significant differences were detected by the ANOVA, a post hoc Bonferroni test was used to make a pairwise comparison of mean values. Variables are presented as mean ± s.d., unless otherwise stated.
Results and Discussion
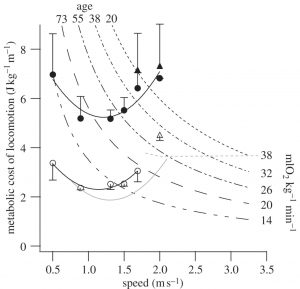
The net mass-specific metabolic cost of locomotion (calculated from gross metabolic rate minus resting metabolic rate divided by speed and expressed relative to unloaded body mass; Cmet; J kg−1 m−1) in armour was 2.1–2.3 times higher than unloaded walking, and 1.9 times higher than unloaded running (p = 0.009; figure 2). This increase was greater than the average 1.4-fold increase in body mass owing to the wearing of armour. Wearing armour increases an individual’s Cmet at any speed for either walking or running. Consequently, for a given rate of metabolic energy expenditure (i.e. effort), the speed of locomotion is lower when wearing armour—including the maximum sustainable speed of locomotion. This limitation is illustrated in figure 2 by the intersection points of the iso-metabolic power curves (representing effort) and the Cmet–speed relationships. For example, for a metabolic power of 32 ml O2 kg−1 min−1 a 38 year old man can sustain a maximum unloaded speed of 2.7 m s−1; however at this metabolic power, he can only walk at a maximum speed of 1.7 m s−1 while wearing armour.
Figure 2: Metabolic cost of locomotion across a range of speeds for walking and running in armour (filled circles and triangles) in comparison with unloaded (open circles and triangles) conditions. Data are means ± s.d. The hyperbolae indicate iso-metabolic power (i.e. combinations of metabolic cost and speed where net metabolic power is the same) expressed as ml O2 kg−1 min−1. The age for which the iso-metabolic power is approximately 80% of the maximum aerobic metabolic rate is indicated; where the hyperbolae intersect the experimental metabolic cost–speed relationship indicates the maximum speed that can be sustained for a significant length of time. The metabolic cost of walking (solid grey line) and running (dashed grey line) previously reported in the literature are plotted for comparison.
Maximum aerobic capacity during exercise decreases with age. Adjacent to the iso-metabolic power curves are the ages of men for which the power is approximately equal to 80 per cent of maximum aerobic metabolic rate—a level that can be sustained for a significant duration. The high energy cost of armoured walking reduces locomotion speed so, when using the same rate of energy expenditure as young men, older men would only be able to sustain very slow speeds (figure 2). For example, when walking in armour at their maximum aerobic metabolic rate, a 38 year old man can sustain a maximum walking speed of 1.7 m s−1; however, a 55 year old man could only sustain a maximum walking speed of 1.4 m s−1.
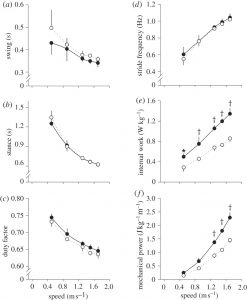
The increase in Cmet of armoured locomotion is much greater than the increase in Cmet observed in humans carrying heavy backpacks: e.g. a 70 per cent increase in Cmet occurs during backpack-loaded walking, and a 50 per cent increase in Cmet in backpack-loaded running [3]. During walking, mechanical work is required to extend the knee in mid-stance, to extend the ankle during the push-off phase at the end of stance and to accelerate the limb at the start of swing. It is likely that the increase in mechanical work associated with moving the lower limbs weighted with armour (sabatons, greaves and cuisses; figure 1b) is a major contributing factor to the increase in Cmet. Stride kinematics were largely unaffected by loading with armour (figure 3). Consequently, the increase in the mechanical cost of swinging the lower limbs during walking is primarily determined by the added mass. The mechanical power required to swing the lower limbs was estimated to increase by approximately 63 per cent across the walking speed range owing to the load of the armour supported by the lower limbs (figure 3; p < 0.001). However, the increase in Cmet is also higher than would be predicted from experiments in which loads have been added to the feet, shanks, thighs and torso (1.9-fold; electronic supplementary material, discussion) [3,8]: wearing armour appears to incur additional energetic costs.
Figure 3: (a) Swing duration, (b) stance duration, (c) duty factor, (d) stride frequency, (e) internal work and (f) mechanical power associated with moving the lower limbs are shown across a range of speeds for armoured and unloaded locomotion. Values are means ± s.d. Symbols indicate that the underlying average value for the armoured (filled circles) condition differs significantly from the corresponding value for the unloaded (open circles) condition. *p < 0.05, †p < 0.01.
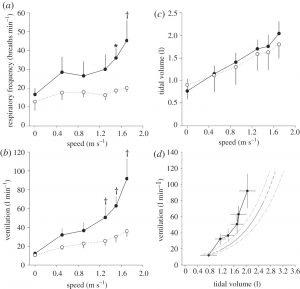
One possibility is that breathing while wearing armour is impaired and, if this is the case, it could limit performance. The high energy demand of locomotion in armour caused ventilation and respiratory frequency to increase dramatically (figure 4), becoming significantly higher than in unloaded conditions at fast walking speeds (p < 0.05). In contrast, tidal volume was not significantly different between armoured and unloaded conditions at any speed (p > 0.3). The highest levels of ventilation achieved by participants during locomotion in armour are similar to those normally observed during intense physical activity (figure 4); however, participants wearing armour sustained these large ventilations at high respiratory frequencies, and small tidal volumes. The breathing pattern observed during locomotion in armour suggests a limitation in inspiratory capacity (i.e. inspiratory reserve volume), and is in agreement with observations reported in subjects with externally applied thoracic restriction [12–15]. The physiological respiratory frequency associated with each ventilation level is naturally adjusted to minimize the sum of the respiratory work necessary to compensate for air turbulence, and the work necessary to expand the chest wall and lungs [16]. For each level of ventilation, wearing armour requires a greater respiratory mechanical work, which increases the activity and energy requirement in the respiratory muscles [17], and consequently results in a reduced respiratory efficiency. The mass added to the chest and the geometrical constraints imposed by the armour are likely to be additional factors contributing to the increase in the metabolic cost of locomotion. Finally, other potential contributors to the increase in Cmet such as frictional losses within the joints between armour components cannot be ruled out.
Figure 4: (a) Respiratory frequency, (b) ventilation and (c) tidal volume are shown across a range of speeds for armoured and unloaded locomotion. (d) Ventilation is shown as a function of tidal volume, and presented in comparison with data taken from the literature (grey line and grey dashed lines indicate average and error values, respectively [11]). Values are means ± s.d. Symbols indicate that the underlying average value for the armoured (filled circles) condition differs significantly from the corresponding value for the unloaded condition (open circles). *p < 0.05, †p < 0.01.
The significant energetic cost of moving in armour is likely to have had a profound limitation on soldiers’ performance, and may have contributed to the outcome of certain battles. For example, during the Battle of Agincourt (1415), heavily armoured French knights advanced towards the English men-at-arms across terrain made extremely muddy from recent ploughing, over-night rain and an earlier French cavalry charge. Exhaustion of the French knights is cited as a contributing factor to their demise at the hands of the more lightly armoured English archers [18]. Similarly, it has been suggested that exhaustion of the French men-at-arms resulting from several days of marching may have impaired their subsequent performance (in armour) and contributed to their defeat by the English army in the Battle of Crécy (1346). Together with numbers and condition of soldiers, equipment availability, battle strategy and terrain, the high energetic cost of movement in armour could have contributed to the outcome of Medieval battles.
References
- Knapik J. J., Reynolds K. L., Harman E. 2004 Soldier load carriage: historical, physiological, biomechanical, and medical aspects. Mil. Med. 169, 45–56.
- Taylor C. R., Heglund N. C., McMahon T. A., Looney T. R. 1980 Energetic cost of generating muscular force during running: a comparison of large and small animals. J. Exp. Biol. 86, 9–18.
- Marsh R. L., Ellerby D. J., Henry H. T., Rubenson J. 2006 The energetic costs of trunk and distal-limb loading during walking and running in guinea fowl Numida meleagris. I. Organismal metabolism and biomechanics. J. Exp. Biol. 209, 2050–2063. doi:10.1242/jeb.02226 (doi:10.1242/jeb.02226)
- Ellerby D. J., Marsh R. L. 2006 The energetic costs of trunk and distal-limb loading during walking and running in guinea fowl Numida meleagris. II. Muscle energy use as indicated by blood flow. J. Exp. Biol. 209, 2064–2075. doi:10.1242/jeb.02227 (doi:10.1242/jeb.02227)
- Quesada P. M., Mengelkoch L. J., Hale R. C., Simon S. R. 2000 Biomechanical and metabolic effects of varying backpack loading on simulated marching. Ergonomics 43, 293–309. doi:10.1080/001401300184413 (doi:10.1080/001401300184413)
- Soule R. G., Goldman R. F. 1969 Energy cost of loads carried on the head, hands, or feet. J. Appl. Physiol. 27, 687–690.
- Soule R. G., Pandolf K. B., Goldman R. F. 1978 Energy expenditure of heavy load carriage. Ergonomics 21, 373–381. doi:10.1080/00140137808931734 (doi:10.1080/00140137808931734)
- Browning R. C., Modica J. R., Kram R., Goswami A. 2007 The effects of adding mass to the legs on the energetics and biomechanics of walking. Med. Sci. Sports Exerc. 39, 515–525. doi:10.1249/mss.0b013e31802b3562 (doi:10.1249/mss.0b013e31802b3562)
- Formenti F., Minetti A. E. 2007 Human locomotion on ice: the evolution of ice-skating energetics through history. J. Exp. Biol. 210, 1825–1833. doi:10.1242/jeb.002162 (doi:10.1242/jeb.002162)
- Minetti A. E. 1998 A model equation for the prediction of mechanical internal work of terrestrial locomotion. J. Biomech. 31, 463–468. doi:10.1016/S0021-9290(98)00038-4 (doi:10.1016/S0021-9290(98)00038-4)
- Neder J. A., Nery L. E., Peres C., Whipp B. J. 2001 Reference values for dynamic responses to incremental cycle ergometry in males and females aged 20 to 80. Am. J. Respir. Crit. Care Med. 164, 1481–1486.
- Legg S. J. 1988 Influence of body armor on pulmonary function. Ergonomics 31, 349–353. doi:10.1080/00140138808966679 (doi:10.1080/00140138808966679)
- Majumdar D., Srivastava K. K., Purkayastha S. S., Pichan G., Selvamurthy W. 1997 Physiological effects of wearing heavy body armour on male soldiers. Int. J. Ind. Ergon. 20, 155–161. doi:10.1016/S0169-8141(96)00057-1 (doi:10.1016/S0169-8141(96)00057-1)
- Coast J. R., Baronas J. L., Morris C., Willeford K. S. 2005 The effect of football shoulder pads on pulmonary function. J. Sport Sci. Med. 4, 367–371.
- Cline C. C., Coast J. R., Arnall D. A. 1999 A chest wall restrictor to study effects on pulmonary function and exercise. 1. Development and validation. Respiration 66, 182–187. doi:10.1159/000029366 (doi:10.1159/000029366)
- Otis A. B., Fenn W. O., Rahn H. 1950 Mechanics of breathing in man. J. Appl. Physiol. 2, 592–607.
- Gonzalez J., Coast J. R., Lawler J. M., Welch H. G. 1999 A chest wall restrictor to study effects on pulmonary function and exercise. 2. The energetics of restrictive breathing. Respiration 66, 188–194. doi:10.1159/000029367 (doi:10.1159/000029367)
- Barker J. 2005 Agincourt: the king, the campaign, the battle. London: Abacus.